【题目】设函数f(x)的定义域为U=(0,+![]() ),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有
),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有![]() >0。
>0。
(1)求f(1)的值;
(2)如果f(x+6)+f(x)>2,求x的取值范围。
参考答案:
【答案】(1) f(1)=0 (2) (2,+![]() )
)
【解析】试题分析: (1)令x1=x2=l,代入f(x1·x2)=f(x1)+f(x2),即可求出f(1)的值;(2)设0<x1<x2,则x2-x1>0.又因为当x1≠x2时, ![]() >0,所以f(x2)-f(x1)>0,即f(x2)>f(x1),所以f(x)在定义域内为增函数. 令x1=x2=4,可求出f(16)=2, 当
>0,所以f(x2)-f(x1)>0,即f(x2)>f(x1),所以f(x)在定义域内为增函数. 令x1=x2=4,可求出f(16)=2, 当![]() 即x>0时,原不等式可化为f[x(x+6)]>f(16),根据函数的单调性解出不等式,即x的范围.
即x>0时,原不等式可化为f[x(x+6)]>f(16),根据函数的单调性解出不等式,即x的范围.
试题解析:
(1)因为对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),
所以令x1=x2=l,得f(1×1)=f(1)+f(1)=2f(1),所以f(1)=0。
(2)设0<x1<x2,则x2-x1>0。
又因为当x1≠x2时, ![]() >0,
>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1),所以f(x)在定义域内为增函数。
令x1=x2=4,得f(4×4)=f(4)+f(4)=1+1=2,即f(16)=2。
当![]() 即x>0时,原不等式可化为f[x(x+6)]>f(16)。
即x>0时,原不等式可化为f[x(x+6)]>f(16)。
又因为f(x)在定义域上为增函数,所以x(x+6)>16,解得x>2或x<-8。
又因为x>0,所以x>2。所以x的取值范围为(2,+![]() )。
)。
点睛:证明函数单调性的一般步骤:(1)取值:在定义域上任取![]() ,并且
,并且![]() (或
(或![]() );(2)作差:
);(2)作差: ![]() ,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断
,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断![]() 的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.
的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2 sin(x+
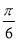 )。
)。(1)若点P(1,-
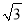 )在角
)在角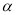 的终边上,求:cos
的终边上,求:cos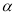 和f(
和f(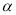 -
-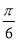 )的值;
)的值;(2)若x
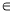 [
[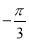 ,
, 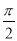 ],求f(x)的值域。
],求f(x)的值域。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市春节7家超市的广告费支出x(万元)和销售额y(万元)数据如下,
超市
A
B
C
D
E
F
G
广告费支出x
1
2
4
6
11
13
19
销售额y
19
32
40
44
52
53
54
(1)请根据上表提供的数据.用最小二乘法求出y关于x的线性回归方程;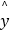 =
= 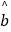 x+
x+ 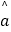
(2)用二次函数回归模型拟合y与x的关系,可得回归方程: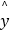 =﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
=﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
参考数据及公式: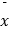 =8,
=8, 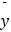 =42.
=42.  xiyi=2794,
xiyi=2794,  x
x 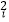 =708,
=708,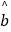 =
= 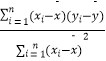 =
= 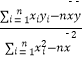 ,
, 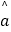 =
= 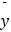 ﹣
﹣ 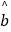 x.
x. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式:y=
 +10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
+10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足
 。
。(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0,
 ],函数f(x)=
],函数f(x)= (2m+
(2m+ )|
)| |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax﹣lnx,F(x)=ex+ax,其中x>0.
(1)若a<0,f(x)和F(x)在区间(0,ln3)上具有相同的单调性,求实数a的取值范围;
(2)设函数h(x)=x2﹣f(x)有两个极值点x1、x2 , 且x1∈(0, ),求证:h(x1)﹣h(x2)>
),求证:h(x1)﹣h(x2)>  ﹣ln2.
﹣ln2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知X的分布列为
X
﹣1
0
1
P



设y=2x+3,则E(Y)的值为( )
A.
B.4
C.﹣1
D.1
相关试题

