【题目】已知函数f(x)=ax﹣lnx,F(x)=ex+ax,其中x>0.
(1)若a<0,f(x)和F(x)在区间(0,ln3)上具有相同的单调性,求实数a的取值范围;
(2)设函数h(x)=x2﹣f(x)有两个极值点x1、x2 , 且x1∈(0, ![]() ),求证:h(x1)﹣h(x2)>
),求证:h(x1)﹣h(x2)> ![]() ﹣ln2.
﹣ln2.
参考答案:
【答案】
(1)解:f′(x)=a﹣ ![]() =
= ![]() ,F′(x)=ex+a,x>0,
,F′(x)=ex+a,x>0,
∵a<0,f′(x)<0在(0,+∞)上恒成立,即f(x)在(0,+∞)上单调递减,
当﹣1≤a<0时,F′(x)>0,即F(x)在(0,+∞)上单调递增,不合题意;
当a<﹣1时,由F′(x)>0,得x>ln(﹣a),由F′(x)<0,得0<x<ln(﹣a),
∴F(x)的单调减区间为(0,ln(﹣a)),单调增区间为(ln(﹣a),+∞).
∵f(x)和F(x)在区间(0,ln3)上具有相同的单调性,
∴ln(﹣a)≥ln3,解得a≤﹣3,
综上,a的取值范围是(﹣∞,﹣3]
(2)解:证明:h(x)=x2﹣ax+lnx,∴h′(x)= ![]() ,(x>0),
,(x>0),
x1x2= ![]() ,则x2=
,则x2= ![]() ,
,
h(x1)﹣h(x2)=lnx1+x12﹣ax1﹣lnx2﹣x22+ax2
=ln ![]() +[x1+x2﹣2(x1+x2)(x1﹣x2)
+[x1+x2﹣2(x1+x2)(x1﹣x2)
=ln2+2lnx1﹣x12+ ![]() ,
,
令g(x1)=ln2+2lnx1﹣x12+ ![]() ,
,
则g′(x)= ![]() ﹣2x1﹣
﹣2x1﹣ ![]() =﹣
=﹣ 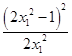 ,
,
∵0<x1< ![]() ,∴g′(x1)<0,
,∴g′(x1)<0,
∴g(x1)在(0, ![]() )上单调递减,
)上单调递减,
∴g(x1)>g( ![]() ),而g(
),而g( ![]() )=
)= ![]() ﹣ln2,
﹣ln2,
即g(x1)> ![]() ﹣ln2,
﹣ln2,
∴h(x1)﹣h(x2)> ![]() ﹣ln2
﹣ln2
【解析】(1)求出函数的导数,通过讨论a的范围,结合函数的单调性确定a的范围即可;(2)先求出h(x1)﹣h(x2)=ln2+2lnx1﹣x12+ ![]() ,构造函数,求出函数的导数,得到函数的单调区间,求出函数的最小值,从而证明结论.
,构造函数,求出函数的导数,得到函数的单调区间,求出函数的最小值,从而证明结论.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式:y=
 +10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
+10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)的定义域为U=(0,+
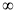 ),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有
),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有 >0。
>0。(1)求f(1)的值;
(2)如果f(x+6)+f(x)>2,求x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足
 。
。(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0,
 ],函数f(x)=
],函数f(x)= (2m+
(2m+ )|
)| |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知X的分布列为
X
﹣1
0
1
P



设y=2x+3,则E(Y)的值为( )
A.
B.4
C.﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(﹣1,1)的密度曲线)的点的个数的估计值为( ) 附:若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
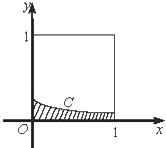
A.1 193
B.1 359
C.2 718
D.3 413 -
科目: 来源: 题型:
查看答案和解析>>【题目】某纺织厂订购一批棉花,其各种长度的纤维所占的比例如下表所示:

(1)请估计这批棉花纤维的平均长度与方差.
(2)如果规定这批棉花纤维的平均长度为4.90厘米,方差不超过1.200,两者允许误差均不超过0.10视为合格产品.请你估计这批棉花的质量是否合格?
相关试题

