【题目】某市春节7家超市的广告费支出x(万元)和销售额y(万元)数据如下,
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)请根据上表提供的数据.用最小二乘法求出y关于x的线性回归方程; ![]() =
= ![]() x+
x+ ![]()
(2)用二次函数回归模型拟合y与x的关系,可得回归方程: ![]() =﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
=﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
参考数据及公式: ![]() =8,
=8, ![]() =42.
=42. ![]() xiyi=2794,
xiyi=2794, ![]() x
x ![]() =708,
=708,![]() =
= 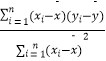 =
= 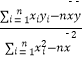 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
参考答案:
【答案】
(1)解:由题意,n=7, ![]() =8,
=8, ![]() =42,
=42, ![]() xiyi=2794,
xiyi=2794, ![]() x
x ![]() =708,
=708,
∴ ![]() =
= 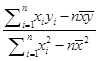 =
= ![]() =1.7,
=1.7,
![]() =
= ![]() ﹣
﹣ ![]() =42﹣1.7×8=28.4,
=42﹣1.7×8=28.4,
∴y关于x的线性回归方程是 ![]() =1.7x+28.4
=1.7x+28.4
(2)解:∵线性回归模型的R2:0.75<0.93,
∴用二次函数回归模型拟合更合适,
当x=3时,得 ![]() =﹣0.17×32+5×3+20=33.47,
=﹣0.17×32+5×3+20=33.47,
预测A超市广告费支出为3万元时销售额为33.47万元
【解析】(1)由题意求出回归系数 ![]() 、
、 ![]() ,写出线性回归方程;(2)根据线性回归模型的相关指数判断用二次函数回归模型更合适,
,写出线性回归方程;(2)根据线性回归模型的相关指数判断用二次函数回归模型更合适,
计算x=3时 ![]() 的值即可.
的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第
 年与年产量
年与年产量 万件之间的关系如下表所示:
万件之间的关系如下表所示:
若
 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一:  =
= =
= =
=  .
.(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少
 ,试根据所建立的函数模型,确定2015年的年产量.
,试根据所建立的函数模型,确定2015年的年产量. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数集X={x1,x2,…,xn}(其中xi>0,i=1,2,…,n,n≥3),若对任意的xk∈X(k=1,2,…,n),都存在xi,xj∈X(xi≠xj),使得下列三组向量中恰有一组共线:
①向量(xi,xk)与向量(xk,xj);②向量(xi,xj)与向量(xj,xk);③向量(xk,xi)与向量(xi,xj),则称X具有性质P。例如{1,2,4}具有性质P。
(1)若{1,3,x)具有性质P,则x的取值为________;
(2)若数集{1,3,x1,x2}具有性质P,则x1+x2的最大值与最小值之积为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2 sin(x+
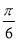 )。
)。(1)若点P(1,-
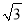 )在角
)在角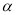 的终边上,求:cos
的终边上,求:cos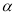 和f(
和f(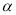 -
-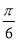 )的值;
)的值;(2)若x
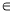 [
[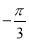 ,
, 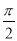 ],求f(x)的值域。
],求f(x)的值域。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式:y=
 +10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
+10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)的定义域为U=(0,+
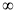 ),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有
),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有 >0。
>0。(1)求f(1)的值;
(2)如果f(x+6)+f(x)>2,求x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足
 。
。(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0,
 ],函数f(x)=
],函数f(x)= (2m+
(2m+ )|
)| |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。
相关试题

