【题目】已知函数![]()
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,解关于
,解关于![]() 的不等式组
的不等式组![]()
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 解集为
解集为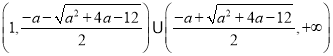 ;
;![]() 解集为
解集为![]()
【解析】
(1)根据解集对应的端点值为函数的零点或者方程的根完成求解;(2)化简不等式,依据二次项系数是否为零分类讨论;(3)先根据![]() 的
的![]() 判断
判断![]() 解的情况,然后再对应分析不等式组的解集.
解的情况,然后再对应分析不等式组的解集.
(1)根据题意可知: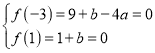 ,解得
,解得![]() ,所以
,所以![]() ;
;
(2)因为![]() 且对任意实数
且对任意实数![]() 都成立
都成立![]() ,所以
,所以![]() 对
对![]() 成立;当
成立;当![]() 时,
时,![]() 成立,符合;当
成立,符合;当![]() 时,
时,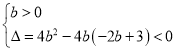 ,解得
,解得![]() ,
,
综上:![]() ;
;
(3)![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 恒成立,所以
恒成立,所以![]() 的解集为:
的解集为:![]() ;当
;当![]() 时,
时,![]() ,此时
,此时![]() 的解集为:
的解集为: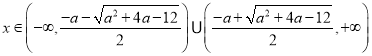 ,若
,若![]() ,
,![]() ,且
,且![]() ,即
,即![]() ,所以
,所以![]() 解集为:
解集为: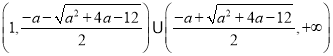 ;当
;当![]() 时,
时,![]() ,即
,即![]() ,则
,则![]() 解集为:
解集为:![]() ;
;
综上:![]() 解集为
解集为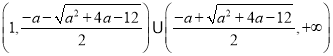 ;
;![]() 解集为
解集为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式
 >2010的n的最小值.
>2010的n的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数
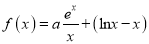 (其中
(其中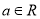 且
且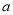 为常数,
为常数, 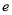 为自然对数的底数,
为自然对数的底数, 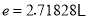 ).
).(Ⅰ)若函数
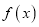 的极值点只有一个,求实数
的极值点只有一个,求实数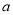 的取值范围;
的取值范围;(Ⅱ)当
 时,若
时,若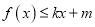 (其中
(其中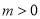 )恒成立,求
)恒成立,求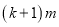 的最小值
的最小值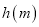 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
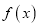 的定义域为D,若函数
的定义域为D,若函数 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域为
上的值域为 ,则称
,则称 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则实数
为“倍缩函数”,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 中,
中, ,且
,且 对任意正整数
对任意正整数 都成立,数列
都成立,数列 的前
的前 项和为
项和为 .
.(1)若
 ,且
,且 ,求
,求 ;
;(2)是否存在实数k,使数列
 是公比不为1的等比数列,且任意相邻三项
是公比不为1的等比数列,且任意相邻三项 按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;(3)若
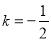 ,求
,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,圆
,圆 .
.(1)若抛物线
 的焦点
的焦点 在圆上,且
在圆上,且 为
为  和圆
和圆 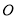 的一个交点,求
的一个交点,求 ;
;(2)若直线
 与抛物线
与抛物线 和圆
和圆 分别相切于点
分别相切于点 ,求
,求 的最小值及相应
的最小值及相应 的值.
的值.
相关试题

