【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
参考答案:
【答案】(1)an=2n-1,n∈N*;(2)n的最小值为10.
【解析】试题分析:本题属于基础题.对已知条件![]() ,用
,用![]() 代替
代替![]() 得
得![]() ,两式相减可得
,两式相减可得![]() ,凑配得
,凑配得![]() ,由此可证得
,由此可证得![]() 是等比数列,从而求出通项公式,这是已知数列前
是等比数列,从而求出通项公式,这是已知数列前![]() 项和与项之间关系的一般处理方法;(2)由(1)可得
项和与项之间关系的一般处理方法;(2)由(1)可得![]() ,采用错位相减法可求出其前
,采用错位相减法可求出其前![]() 项和
项和![]()
![]() ,不等式>2 010就转化为
,不等式>2 010就转化为![]() ,可知n的最小值是10.
,可知n的最小值是10.
试题解析:(1)因为Sn+n=2an,所以Sn-1=2an-1-(n-1)(n≥2,n∈N*).两式相减,得an=2an-1+1.
所以an+1=2(an-1+1)(n≥2,n∈N*),所以数列{an+1}为等比数列.
因为Sn+n=2an,令n=1得a1=1.
a1+1=2,所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,所以bn=(2n+1)·2n.
所以Tn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n, ①
2Tn=3×22+5×23+…+(2n-1)·2n+(2n+1)·2n+1, ②
①-②,得-Tn=3×2+2(22+23+…+2n)-(2n+1)·2n+1
=6+2×-(2n+1)·2n+1
=-2+2n+2-(2n+1)·2n+1=-2-(2n-1)·2n+1.
所以Tn=2+(2n-1)·2n+1.
若>2 010,
则>2 010,即2n+1>2 010.
由于210=1 024,211=2 048,所以n+1≥11,即n≥10.
所以满足不等式>2 010的n的最小值是10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI
0~50
51~100
101~150
151~200
201~300
300以上
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+1,g(x)=2alnx+1(a∈R)
(1)求函数h(x)=f(x)
 g(x)的极值;
g(x)的极值;(2)当a=e时,是否存在实数k,m,使得不等式g(x)≤ kx+m ≤f(x)恒成立?若存在,请求实数k,m的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与抛物线
与抛物线 交于
交于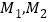 两点,直线
两点,直线 与
与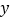 轴交于点
轴交于点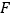 ,且直线
,且直线 恰好平分
恰好平分 .
.
(1)求
 的值;
的值;(2)设
 是直线
是直线 上一点,直线
上一点,直线 交抛物线于另一点
交抛物线于另一点 ,直线
,直线 交直线
交直线 于点
于点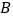 ,求
,求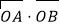 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数
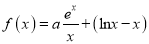 (其中
(其中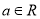 且
且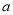 为常数,
为常数, 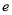 为自然对数的底数,
为自然对数的底数, 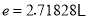 ).
).(Ⅰ)若函数
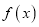 的极值点只有一个,求实数
的极值点只有一个,求实数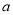 的取值范围;
的取值范围;(Ⅱ)当
 时,若
时,若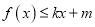 (其中
(其中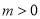 )恒成立,求
)恒成立,求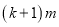 的最小值
的最小值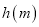 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
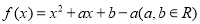
(1)若关于
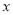 的不等式
的不等式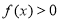 的解集为
的解集为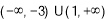 ,求实数
,求实数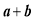 的值;
的值;(2)设
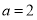 ,若不等式
,若不等式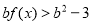 对任意实数
对任意实数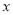 都成立,求实数
都成立,求实数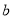 的取值范围;
的取值范围;(3)设
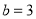 ,解关于
,解关于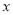 的不等式组
的不等式组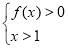
相关试题

