【题目】已知数列![]() 中,
中,![]() ,且
,且![]() 对任意正整数
对任意正整数![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在实数k,使数列![]() 是公比不为1的等比数列,且任意相邻三项
是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
(3)若![]() ,求
,求![]() .
.
参考答案:
【答案】(1) ![]() ;(2) 满足要求的实数
;(2) 满足要求的实数![]() 有且仅有一个,
有且仅有一个,![]() ;(3)
;(3) ![]()

![]() .
.
【解析】
(1)先根据等差中项判定数列类型,再求解![]() 的值;(2)假设存在
的值;(2)假设存在![]() 满足后,先计算
满足后,先计算![]() 通项公式,再考虑相邻三项排列后成等差数然后计算
通项公式,再考虑相邻三项排列后成等差数然后计算![]() 的值,注意分类;(3)先化简递推公式,根据递推公式进行奇偶分项讨论.
的值,注意分类;(3)先化简递推公式,根据递推公式进行奇偶分项讨论.
(1)![]() 时,
时,![]() ,
,![]() ,
,
所以数列![]() 是等差数列,
是等差数列,
此时首项![]() ,公差
,公差![]() ,
,
数列![]() 的前
的前![]() 项和是
项和是![]() ,
,
故![]() ,得
,得![]() ;
;
(2)设数列![]() 是等比数列,则它的公比
是等比数列,则它的公比![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
①若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,
,
解得![]() ,不合题意;
,不合题意;
②若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,
,
化简得:![]() ,
,
解得![]() ,
,![]() (舍去);
(舍去);![]() ;
;
③若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,
,
化简得:![]() ,解得
,解得![]() ;
;![]() ;
;
综上可得,满足要求的实数![]() 有且仅有一个,
有且仅有一个,![]() ;
;
(3)![]() 则
则![]() ,
,
![]() ,
,![]() ,
,
当![]() 是偶数时,
是偶数时,
![]()
![]()
![]() ,
,
当![]() 是奇数时,
是奇数时,
![]()
![]()
![]()
![]()
![]() ,
,![]() 也适合上式,
也适合上式,
综上可得,![]()

![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
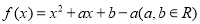
(1)若关于
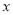 的不等式
的不等式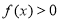 的解集为
的解集为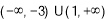 ,求实数
,求实数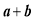 的值;
的值;(2)设
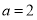 ,若不等式
,若不等式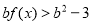 对任意实数
对任意实数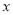 都成立,求实数
都成立,求实数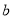 的取值范围;
的取值范围;(3)设
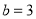 ,解关于
,解关于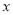 的不等式组
的不等式组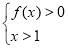
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
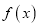 的定义域为D,若函数
的定义域为D,若函数 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域为
上的值域为 ,则称
,则称 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则实数
为“倍缩函数”,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,圆
,圆 .
.(1)若抛物线
 的焦点
的焦点 在圆上,且
在圆上,且 为
为  和圆
和圆 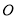 的一个交点,求
的一个交点,求 ;
;(2)若直线
 与抛物线
与抛物线 和圆
和圆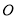 分别相切于点
分别相切于点 ,求
,求 的最小值及相应
的最小值及相应 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量
 与尺寸
与尺寸 之间近似满足关系式
之间近似满足关系式 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:尺寸

38
48
58
68
78
88
质量

16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比

0.442
0.392
0.357
0.329
0.308
0.290
(Ⅰ)现从抽取的6件合格产品中再任选3件,求恰好取到2件优等品的概率;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
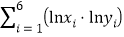



75.3
24.6
18.3
101.4
(i)根据所给统计量,求
 关于
关于 的回归方程;
的回归方程;(ii)已知优等品的收益
 (单位:千元)与
(单位:千元)与 的关系
的关系 ,则当优等品的尺寸为
,则当优等品的尺寸为 为何值时,收益
为何值时,收益 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)附:对于样本
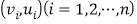 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
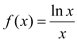 ,
, .
.(I)求函数
 的最大值;
的最大值;(II)当
 时,函数
时,函数 有最小值,记
有最小值,记 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域.
相关试题

