【题目】已知下列四个命题:
①函数f(x)= ![]() x﹣lnx(x>0),则y=f(x)在区间(
x﹣lnx(x>0),则y=f(x)在区间( ![]() ,1)内无零点,在区间(1,e)内有零点;
,1)内无零点,在区间(1,e)内有零点;
②函数f(x)=log2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() 不都是奇函数;
不都是奇函数;
③若函数f(x)满足f(x﹣1)=﹣f(x+1),且f(1)=2,则f(7)=﹣2;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
其中正确命题的序号是 .
参考答案:
【答案】①③④
【解析】解:①函数f(x)= ![]() x﹣lnx(x>0),
x﹣lnx(x>0),
则y=f(x)在区间( ![]() ,1)内f(x)>0恒成立,此时函数无零点,
,1)内f(x)>0恒成立,此时函数无零点,
f(1)f(e)<0,故在区间(1,e)内有零点;
故①正确;
②函数f(x)=log2(x+ ![]() )定义域为R,关于原点对称,
)定义域为R,关于原点对称,
f(﹣x)+f(x)=log2(﹣x+ ![]() )+log2(x+
)+log2(x+ ![]() )=log21=0,
)=log21=0,
即f(﹣x)=﹣f(x),故为奇函数;
g(x)=1+ ![]() =
= ![]() 定义域为{x|x≠0},关于原点对称,
定义域为{x|x≠0},关于原点对称,
g(﹣x)= ![]() =
= ![]() =﹣g(x),故为奇函数;
=﹣g(x),故为奇函数;
故②错误;
③若函数f(x)满足f(x﹣1)=﹣f(x+1),且f(1)=2,
则f(1)=﹣f(3)=f(5)=﹣f(7),
∴f(7)=﹣2;
故③正确;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则logax1=﹣logax2 ,
即logax1+logax2=logax1x2=0,即x1x2=1,
故④正确;
所以答案是:①③④.
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有
 名,则
名,则 的值为( )
的值为( )A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
附: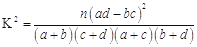
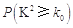
0.100
0.050
0.010
0.001
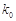
2.706
3.841
6.635
10.828
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下 列联表:
列联表:接受挑战
不接受挑战
合计
男性
50
10
60
女性
25
15
40
合计
75
25
100
根据表中数据,是否有99%的把握认为“冰桶挑战赛与受邀者的性别有关”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.﹣16
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知O、A、B三地在同一水平面内,A地在O地正东方向2km处,B地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过
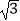 km的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
km的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
A.1-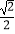
B.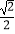
C.1-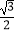
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为
 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为 。
。(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
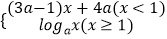 是(﹣∞,+∞)上的减函数,那么a的取值范围是
是(﹣∞,+∞)上的减函数,那么a的取值范围是
相关试题

