【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)消去![]() 得到
得到![]() ,进而得到直线的极坐标方程,根据直角坐标与极坐标的互化公式,即可化简得到圆的极坐标方程;
,进而得到直线的极坐标方程,根据直角坐标与极坐标的互化公式,即可化简得到圆的极坐标方程;
(Ⅱ)由直线的极坐标方程与曲线的极坐标方程联立,得两根为![]() ,
, ![]() ,得到弦长
,得到弦长![]() ,得到三角形的面积.
,得到三角形的面积.
试题解析:(Ⅰ)由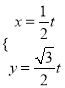 消去
消去![]() 得到
得到![]() ,则
,则![]() ,∴
,∴![]() ,
,
所以直线l的极坐标方程为![]() (
(![]() )
)
曲线![]() ,则
,则![]()
则曲线C的极坐标方程为![]()
(Ⅱ)由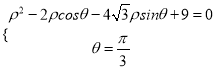 ,得到
,得到![]() ,设其两根为
,设其两根为![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,∴
,∴![]() ,
,
∵点P的极坐标为![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
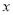 千件,需另投入成本为
千件,需另投入成本为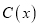 ,当年产量不足80千件时,
,当年产量不足80千件时, 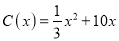 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, 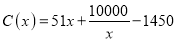 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(Ⅰ)写出年利润
 (万元)关于年产量
(万元)关于年产量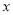 (千件)的函数解析式;
(千件)的函数解析式;(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“足寒伤心,民寒伤国”,精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对石山区乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量
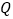 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费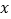 万元之间的函数关系为
万元之间的函数关系为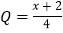 (其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本
(其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本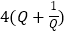 万元(不包含推广促销费用),若加工后的每件成品的销售价格定为
万元(不包含推广促销费用),若加工后的每件成品的销售价格定为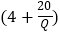 元/件.
元/件.(1)试将该批产品的利润
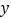 万元表示为推广促销费
万元表示为推广促销费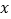 万元的函数;(利润
万元的函数;(利润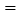 销售额
销售额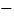 成本
成本 推广促销费)
推广促销费)(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=2,直线CA与平面ABD所成角的正弦值为
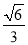 ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.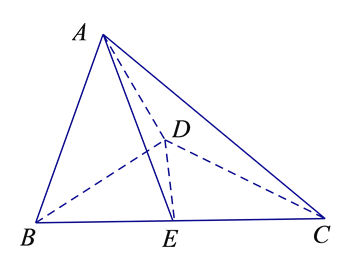
-
科目: 来源: 题型:
查看答案和解析>>【题目】设各项均为正数的数列
 的前
的前 项和为
项和为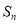 ,满足
,满足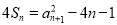 ,且
,且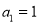 ,公比大于1的等比数列
,公比大于1的等比数列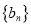 满足
满足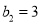 ,
, 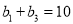 .
.(1)求证数列
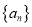 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;(2)若
 ,求数列
,求数列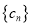 的前
的前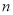 项和
项和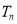 ;
;(3)在(2)的条件下,若
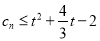 对一切正整数
对一切正整数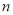 恒成立,求实数
恒成立,求实数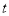 的取值
的取值 -
科目: 来源: 题型:
查看答案和解析>>【题目】据市场分析,某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本
 (万元)可以看成月产量
(万元)可以看成月产量 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.(1)写出月总成本
 (万元)关于月产量
(万元)关于月产量 (吨)的函数关系;
(吨)的函数关系;(2)已知该产品的销售价为每吨1.6万元,那么月产量为多少时,可获最大利润.
(3)当月产量为多少吨时,每吨平均成本最低,最低成本是多少万元?
相关试题

