【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,侧面
为正方形,侧面![]() 底面
底面![]() ,
,![]() 为
为![]() 中点,
中点,![]() .
.

(I)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() //平面
//平面![]() ,指出点
,指出点![]() 的位置并证明;
的位置并证明;
(II)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(I)存在,![]() 为线段
为线段![]() 的中点;(II)
的中点;(II)![]() .
.
【解析】
试题分析:(I)连结![]() ,由三角形的中位线长定理可知
,由三角形的中位线长定理可知![]() ,再由线面平行的判定定理可证得
,再由线面平行的判定定理可证得![]() //平面
//平面![]() ;(II)取
;(II)取![]() 中点
中点![]() ,则
,则![]() ,
,![]() ,以
,以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,![]() 是平面
是平面![]() 的一个法向量,设平面
的一个法向量,设平面![]() 的一个法向量是
的一个法向量是![]() ,再求
,再求![]() 即可.
即可.
试题解析:
(I)存在点![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
证明:如图,连结![]() ,
,
因为底面![]() 是正方形,所以
是正方形,所以![]() 与
与![]() 互相平分,
互相平分,
又因为![]() 是
是![]() 中点,所以
中点,所以![]() 是
是![]() 中点,
中点,
所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() ;
;
(II)取![]() 中点
中点![]() ,
,
在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
因为面![]() 底面
底面![]() ,且面
,且面![]() 面
面![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
因为![]() ,所以
,所以![]() ,则
,则![]() ,
,
 ,
,
于是 ,
,
因为![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的一个法向量是
的一个法向量是![]() ,
,
因为 ,所以
,所以 ,即
,即 ,
,
令![]() ,则
,则![]() ,
,
所以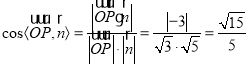 ,
,
由图可知,二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的一段图象如图所示.
的一段图象如图所示.
(1)求函数
 的解析式;
的解析式;(2)将函数
 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与
与函数
 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)当
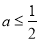 时,讨论函数
时,讨论函数 的单调性;
的单调性;(2)设
 ,当
,当 时,若对任意
时,若对任意 ,存在
,存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为
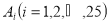 由右边的程序运行后,输出
由右边的程序运行后,输出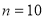 .据此解答如下问题:
.据此解答如下问题: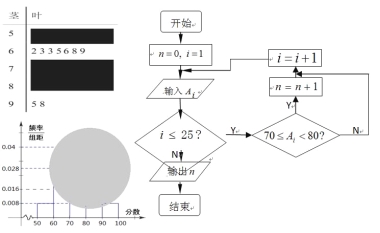
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量 (单位:
(单位:  )和年利润
)和年利润 (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费 和年销售量
和年销售量 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

(1)根据散点图判断,
 与
与 哪一个适宜作为年销售量
哪一个适宜作为年销售量 关于年宣传费
关于年宣传费 的回归方程类型?(给出判断即可,不必说出理由);
的回归方程类型?(给出判断即可,不必说出理由);(2)根据(1)的判断结果及表中数据,建立
 关于
关于 的回归方程;
的回归方程;(3)已知这种产品的年利润
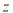 与
与 的关系为
的关系为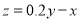 ,根据(2)的结果求:年宣传费
,根据(2)的结果求:年宣传费 为何值时,年利润最大?
为何值时,年利润最大?附:对于一组数据
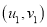 ,
,  ,…
,…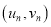 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 上有一个动点
上有一个动点 ,过点
,过点 作直线
作直线 垂直于
垂直于 轴,动点
轴,动点 在
在 上,且满足
上,且满足 (
( 为坐标原点),记点
为坐标原点),记点 的轨迹为
的轨迹为 .
.(I)求曲线
 的方程;
的方程;(II)若直线
 是曲线
是曲线 的一条切线,当点
的一条切线,当点 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富高学生的课外生活,某校要组建数学计算机航空模型3个兴趣小组,小明要选报其中的2个,则包含的样本点共有( )
A.1个B.2个C.3个D.4个
相关试题

