【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() 和
和![]() ;当
;当![]() 时,减区间为
时,减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先求得函数![]() 的定义域与导函数,然后分
的定义域与导函数,然后分![]() 、
、![]() 、
、![]() 求得函数的单调区间;(2)首先结合(1)求得当
求得函数的单调区间;(2)首先结合(1)求得当![]() 时
时![]() 的最小值,然后利用分离参数法得
的最小值,然后利用分离参数法得![]() ,由此令
,由此令![]() ,从而根据
,从而根据![]() 的单调性求得其最小值,进而求得
的单调性求得其最小值,进而求得![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]()
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
由![]() 和
和![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
综上所述当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() 和
和![]() ,
,
当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() .
.
(2)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() ,
,![]() ,依题意有
,依题意有![]() ,
,
∵![]()
![]()
![]() 在
在![]() 上有解,
上有解,
令![]() ,知
,知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴![]()
∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.
或用![]() ,而
,而![]() ,对
,对![]() 分三种情况:
分三种情况:
①
![]() 无解;
无解;
②
![]()
![]() ;
;
③
![]()
![]() .
.
综上:∴![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.

(1)求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;(2)求当天的利润不低于750元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
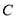 的焦点在原点
的焦点在原点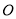 ,左焦点
,左焦点 ,左顶点
,左顶点 ,上顶点
,上顶点 ,
, 的周长为
的周长为 ,
, 的面积为
的面积为 .
.(I)求椭圆
 的标准方程;
的标准方程;(II)是否存在与椭圆
 交于
交于 两点的直线
两点的直线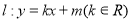 使得
使得 成立?若存在,求出实数
成立?若存在,求出实数 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的一段图象如图所示.
的一段图象如图所示.
(1)求函数
 的解析式;
的解析式;(2)将函数
 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与
与函数
 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为
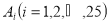 由右边的程序运行后,输出
由右边的程序运行后,输出 .据此解答如下问题:
.据此解答如下问题: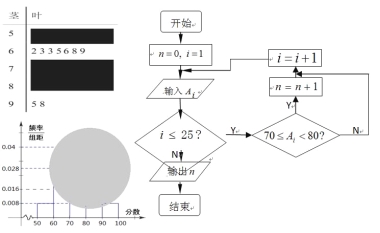
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为正方形,侧面
为正方形,侧面 底面
底面 ,
, 为
为 中点,
中点, .
.
(I)在线段
 上是否存在点
上是否存在点 ,使得
,使得 //平面
//平面 ,指出点
,指出点 的位置并证明;
的位置并证明;(II)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量 (单位:
(单位:  )和年利润
)和年利润 (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费 和年销售量
和年销售量 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

(1)根据散点图判断,
 与
与 哪一个适宜作为年销售量
哪一个适宜作为年销售量 关于年宣传费
关于年宣传费 的回归方程类型?(给出判断即可,不必说出理由);
的回归方程类型?(给出判断即可,不必说出理由);(2)根据(1)的判断结果及表中数据,建立
 关于
关于 的回归方程;
的回归方程;(3)已知这种产品的年利润
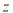 与
与 的关系为
的关系为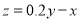 ,根据(2)的结果求:年宣传费
,根据(2)的结果求:年宣传费 为何值时,年利润最大?
为何值时,年利润最大?附:对于一组数据
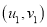 ,
,  ,…
,…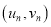 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,  .
.
相关试题

