【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.

![]() 证明:
证明:![]() ;
;
![]() 证明:
证明:![]() ;
;
![]() 是否存在一点
是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)当D为![]() 中点.
中点.
【解析】
![]() 根据线面垂直的性质定理证明
根据线面垂直的性质定理证明![]() 面
面![]() 即可.
即可.
![]() 建立空间坐标系,求出直线对应的向量,利用向量垂直的关系进行证明.
建立空间坐标系,求出直线对应的向量,利用向量垂直的关系进行证明.
![]() 求出平面的法向量,利用向量法进行求解即可.
求出平面的法向量,利用向量法进行求解即可.
![]() 证明:
证明:![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 面
面![]() .
.
又![]() 面
面![]() ,
,![]() ,
,
![]() 以A为原点建立如图所示的空间直角坐标系
以A为原点建立如图所示的空间直角坐标系![]() ,
,

则有![]() ,
,
设![]() 且
且![]() ,
,
即![]() y,
y,![]() ,0,
,0,![]() ,则
,则![]() 0,
0,![]() ,
,![]() ,
,
![]() ,
,![]() ,所以
,所以![]() ;
;
![]() 结论:存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为
结论:存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为![]() ,理由如下:
,理由如下:
由题可知面ABC的法向量![]() ,设面DEF的法向量为
,设面DEF的法向量为![]() ,
,
则 ,
,
![]() ,
,
 ,即
,即 ,
,
令![]() ,则
,则![]() .
.
![]() 平面DEF与平面ABC所成锐二面角的余弦值为
平面DEF与平面ABC所成锐二面角的余弦值为![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() 或
或![]() 舍
舍![]() ,
,
所以当D为![]() 中点时满足要求.
中点时满足要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 过点
过点 ,
, ,且圆心
,且圆心 在直线
在直线 上,过点
上,过点 作直线
作直线 与圆
与圆 :
: 交于两点
交于两点 ,
, .
.(1)求圆
 的方程;
的方程;(2)当
 时,若
时,若 于圆
于圆 交于
交于 ,
, 且
且 ,求直线
,求直线 的方程;
的方程;(3)若点
 恰好是线段
恰好是线段 的中点,求实数
的中点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
, ,
, ,
, ,函数
,函数 ,
, 的最小正周期为
的最小正周期为 .
.(1)求
 的单调增区间;
的单调增区间;(2)方程
 ;在
;在 上有且只有一个解,求实数n的取值范围;
上有且只有一个解,求实数n的取值范围;(3)是否存在实数m满足对任意x1∈[-1,1],都存在x2∈R,使得
 +
+ +m(
+m( -
- )+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
)+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题,其中真命题的个数是( )
①若“
 或
或 ”是假命题,则“
”是假命题,则“ 且
且 ”是真命题;
”是真命题;②命题“若
 ,则
,则 或
或 ”为真命题;
”为真命题;③已知空间任意一点
 和不共线的三点
和不共线的三点 ,
, ,
, ,若
,若 ,则
,则 ,
, ,
, ,
, 四点共面;
四点共面;④直线
 与双曲线
与双曲线 交于
交于 ,
, 两点,若
两点,若 ,则这样的直线有3条;
,则这样的直线有3条;A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形
中,四边形 是菱形,
是菱形,  ,平面
,平面 平面
平面
 在棱
在棱 上运动.
上运动.
(1)当
 在何处时,
在何处时,  平面
平面 ;
;(2)已知
 为
为 的中点,
的中点,  与
与 交于点
交于点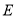 ,当
,当 平面
平面 时,求三棱锥
时,求三棱锥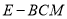 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若acos2
 +ccos2
+ccos2 =
= b.
b.(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
相关试题

