【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先得到从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次的基本事件的总数,再得到两个小球号码相加之和为4即中二等奖的基本事件数,代入古典概型的概率公式求解.
(2)先得到中奖的基本事件数,进而得到未中奖的基本事件数,代入公式求解.
(1)从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次的基本事件有![]() 种,
种,
两个小球号码相加之和为4即中二等奖的基本事件有![]() ,共3种,
,共3种,
所以中二等奖的概率为![]() .
.
(2)两个小球号码相加之和等于6的基本事件有![]() ,共1种,
,共1种,
两个小球号码相加之和等于5的基本事件有![]() ,共2种,
,共2种,
两个小球号码相加之和等于3的基本事件有![]() ,共4种,
,共4种,
所以未中奖的概率![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.
 证明:
证明: ;
; 证明:
证明: ;
;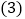 是否存在一点
是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形
中,四边形 是菱形,
是菱形,  ,平面
,平面 平面
平面
 在棱
在棱 上运动.
上运动.
(1)当
 在何处时,
在何处时,  平面
平面 ;
;(2)已知
 为
为 的中点,
的中点,  与
与 交于点
交于点 ,当
,当 平面
平面 时,求三棱锥
时,求三棱锥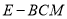 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若acos2
 +ccos2
+ccos2 =
= b.
b.(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组
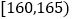 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 也为抛物线
也为抛物线 的焦点.(1)若
的焦点.(1)若 为椭圆
为椭圆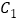 上两点,且线段
上两点,且线段 的中点为
的中点为 ,求直线
,求直线 的斜率;
的斜率;(2)若过椭圆
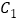 的右焦点
的右焦点 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于 和
和 ,设线段
,设线段 的长分别为
的长分别为 ,证明
,证明 是定值.
是定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级
初二年级
初三年级
女生
373
x
y
男生
377
370
z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y
 245,z
245,z 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
相关试题

