【题目】已知向量![]() ,
,![]() ,
,![]() ,
,![]() ,函数
,函数![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的单调增区间;
的单调增区间;
(2)方程![]() ;在
;在![]() 上有且只有一个解,求实数n的取值范围;
上有且只有一个解,求实数n的取值范围;
(3)是否存在实数m满足对任意x1∈[-1,1],都存在x2∈R,使得![]() +
+![]() +m(
+m(![]() -
-![]() )+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
)+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
参考答案:
【答案】(1)![]() ,
,![]() (2)
(2)![]() 或
或![]() (3)存在,且m取值范围为
(3)存在,且m取值范围为![]()
【解析】
(1)函数![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .可得
.可得![]() ,即可求解
,即可求解![]() 的单调增区间.
的单调增区间.
(2)根据x在![]() 上求解
上求解![]() 的值域,即可求解实数n的取值范围;
的值域,即可求解实数n的取值范围;
(3)由题意,求解![]() 的最小值,利用换元法求解
的最小值,利用换元法求解![]() 的最小值,即可求解m的范围.
的最小值,即可求解m的范围.
(1)函数f(x)![]()
![]() 1=2sin2(ωx
1=2sin2(ωx![]() )
)![]() cos(2ωx)﹣1
cos(2ωx)﹣1
=sin(2ωx)![]() cos(2ωx)
cos(2ωx)
=2sin(2ωx![]() )
)
∵f(x)的最小正周期为π.ω>0
∴![]() ,
,
∴ω=1.
那么f(x)的解析式f(x)=2sin(2x![]() )
)
令![]() 2x
2x![]() ,k∈Z
,k∈Z
得:![]() x
x![]()
∴f(x)的单调增区间为[![]() ,
,![]() ],k∈Z.
],k∈Z.
(2)方程f(x)﹣2n+1=0;在[0,![]() ]上有且只有一个解,
]上有且只有一个解,
转化为函数y=f(x)+1与函数y=2n只有一个交点.
∵x在[0,![]() ]上,
]上,
∴![]() (2x
(2x![]() )
)![]()
那么函数y=f(x)+1=2sin(2x![]() )+1的值域为[
)+1的值域为[![]() ,2],结合图象可知
,2],结合图象可知
函数y=f(x)+1与函数y=2n只有一个交点.
那么![]() 2n<1或2n=2,
2n<1或2n=2,
可得![]() 或n=1.
或n=1.
(3)由(1)可知f(x)=2sin(2x![]() )
)
∴f(x2)min=﹣2.
实数m满足对任意x1∈[﹣1,1],都存在x2∈R,
使得![]() m(
m(![]() )+1>f(x2)成立.
)+1>f(x2)成立.
即![]() m(
m(![]() )+1>﹣2成立
)+1>﹣2成立
令y![]() m(
m(![]() )+1
)+1
设![]() t,那么
t,那么![]() (
(![]() )2+2=t2+2
)2+2=t2+2
∵x1∈[﹣1,1],
∴t∈[![]() ,
,![]() ],
],
可得t2+mt+5>0在t∈[![]() ,
,![]() ]上成立.
]上成立.
令g(t)=t2+mt+5>0,
其对称轴t![]()
∵t∈[![]() ,
,![]() ]上,
]上,
∴①当![]() 时,即m≥3时,g(t)min=g(
时,即m≥3时,g(t)min=g(![]() )
)![]() ,解得
,解得![]() ;
;
②当![]() ,即﹣3<m<3时,g(t)min=g(
,即﹣3<m<3时,g(t)min=g(![]() )
)![]() 0,解得﹣3<m<3;
0,解得﹣3<m<3;
③当![]() ,即m≤﹣3时,g(t)min=g(
,即m≤﹣3时,g(t)min=g(![]() )
)![]() 0,解得
0,解得![]() m≤﹣3;
m≤﹣3;
综上可得,存在m,可知m的取值范围是(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
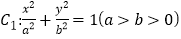 的离心率为
的离心率为 ,抛物线
,抛物线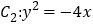 的准线被椭圆
的准线被椭圆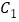 截得的线段长为
截得的线段长为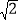 .
.(1)求椭圆
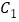 的方程;
的方程;(2)如图,点
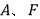 分别是椭圆
分别是椭圆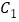 的左顶点、左焦点直线
的左顶点、左焦点直线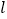 与椭圆
与椭圆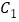 交于不同的两点
交于不同的两点 (
( 都在
都在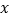 轴上方).且
轴上方).且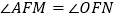 .证明:直线
.证明:直线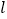 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.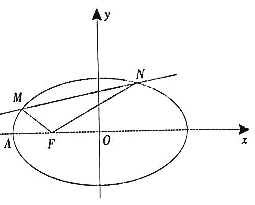
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
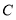 :
: ,直线
,直线 :
: .
.(1)求直线
 所过定点
所过定点 的坐标;
的坐标;(2)求直线
 被圆
被圆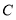 所截得的弦长最短时
所截得的弦长最短时 的值;
的值;(3)已知点
 ,在直线
,在直线 (
(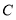 为圆心)上存在定点
为圆心)上存在定点 (异于点
(异于点 ),满足:对于圆
),满足:对于圆 上任一点
上任一点 ,都有
,都有 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点 的坐标及该常数.
的坐标及该常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 过点
过点 ,
, ,且圆心
,且圆心 在直线
在直线 上,过点
上,过点 作直线
作直线 与圆
与圆 :
: 交于两点
交于两点 ,
, .
.(1)求圆
 的方程;
的方程;(2)当
 时,若
时,若 于圆
于圆 交于
交于 ,
, 且
且 ,求直线
,求直线 的方程;
的方程;(3)若点
 恰好是线段
恰好是线段 的中点,求实数
的中点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题,其中真命题的个数是( )
①若“
 或
或 ”是假命题,则“
”是假命题,则“ 且
且 ”是真命题;
”是真命题;②命题“若
 ,则
,则 或
或 ”为真命题;
”为真命题;③已知空间任意一点
 和不共线的三点
和不共线的三点 ,
, ,
, ,若
,若 ,则
,则 ,
, ,
, ,
, 四点共面;
四点共面;④直线
 与双曲线
与双曲线 交于
交于 ,
, 两点,若
两点,若 ,则这样的直线有3条;
,则这样的直线有3条;A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.
 证明:
证明: ;
; 证明:
证明: ;
; 是否存在一点
是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形
中,四边形 是菱形,
是菱形,  ,平面
,平面 平面
平面
 在棱
在棱 上运动.
上运动.
(1)当
 在何处时,
在何处时,  平面
平面 ;
;(2)已知
 为
为 的中点,
的中点,  与
与 交于点
交于点 ,当
,当 平面
平面 时,求三棱锥
时,求三棱锥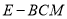 的体积.
的体积.
相关试题

