【题目】已知![]() .
.
(1)若函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:⑴求出![]() 的导函数,令导函数小于
的导函数,令导函数小于![]() 得到不等式的解集,得到相应方程的两个根,将根代入求出
得到不等式的解集,得到相应方程的两个根,将根代入求出![]() 的值,得到函数
的值,得到函数![]() 的解析式,求出
的解析式,求出![]() 的导数在
的导数在![]() 的值即曲线的切线斜率,利用点斜式求出切线的方程
的值即曲线的切线斜率,利用点斜式求出切线的方程
⑵求出不等式,分离出参数![]() ,构造函数
,构造函数![]() ,利用导数求出
,利用导数求出![]() 的最大值,令
的最大值,令![]() 大于等于最大值,求出
大于等于最大值,求出![]() 的范围;
的范围;
解析:(1)![]() ,由题意,知
,由题意,知![]() 的解集是
的解集是![]() ,
,
即方程![]() 的两根分别是
的两根分别是![]() .
.
将![]() 或
或![]() 代入方程
代入方程![]() ,得
,得![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() 的图像在点
的图像在点![]() 处的切线斜率
处的切线斜率![]() ,
,
∴函数![]() 的图像在点
的图像在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() ;
;
(2)∵![]() 恒成立,
恒成立,
即![]() 对一切
对一切![]() 恒成立,
恒成立,
整理可得![]() 对一切
对一切![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() (舍),
(舍),
当![]() 时,
时, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 单调递减,
单调递减,
∴当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,∴
,∴![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=
 (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为  ,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( ) 
A.6平方米
B.9平方米
C.12平方米
D.15平方米 -
科目: 来源: 题型:
查看答案和解析>>【题目】贵阳与凯里两地相距约200千米,一辆货车从贵阳匀速行驶到凯里,规定速度不得超过100千米
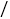 时,已知货车每小时的运输成本
时,已知货车每小时的运输成本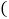 以元为单位
以元为单位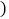 由可变部分和固定部分组成:可变部分与速度
由可变部分和固定部分组成:可变部分与速度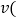 千米
千米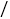 时
时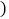 的平方成正比,比例系数为
的平方成正比,比例系数为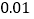 ;固定部分为64元.
;固定部分为64元. 把全程运输成本
把全程运输成本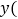 元
元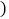 表示为速度
表示为速度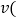 千米
千米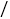 时
时 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域; 为了使全程运输成本最小,货车应以多大速度行驶?
为了使全程运输成本最小,货车应以多大速度行驶? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线C:
 ﹣
﹣  =1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若
=1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若  的最大值小于0,则双曲线C的离心率e的取值范围为 .
的最大值小于0,则双曲线C的离心率e的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.

(1)求f(x)的解析式,并求函数f(x)在[﹣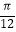 ,
,  ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
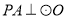 所在的平面,
所在的平面, 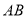 是
是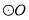 的直径,
的直径, 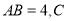 是
是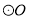 上一点,且
上一点,且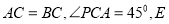 是
是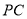 中点,
中点,  为
为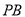 中点.
中点.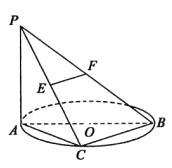
(1)求证:
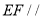 面
面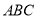 ;
;(2)求证:
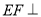 面
面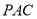 ;
;(3)求三棱锥
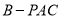 的体积.
的体积.
相关试题

