【题目】已知函数f(x)=ex-x2+a,x∈R的图象在x=0处的切线方程为y=bx.(e≈2.718 28)
(1)求函数f(x)的解析式;
(2)当x∈R时,求证:f(x)≥-x2+x;
(3)若f(x)>kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
参考答案:
【答案】(1) 解析式为f(x)=ex-x2-1;(2)见解析;(3)实数k的取值范围为(-∞,e-2).
【解析】试题分析:(1)根据导数几何意义得![]() ,再结合
,再结合![]() ,解方程组得
,解方程组得![]() (2)作差函数,根据导数求其单调性,根据单调性确定其最小值,即证得不等式,(3)先分离变量,转化为求对应函数g(x)=
(2)作差函数,根据导数求其单调性,根据单调性确定其最小值,即证得不等式,(3)先分离变量,转化为求对应函数g(x)=![]() 的最小值,再根据导数求g(x)单调性,由单调性确定其最小值取法,即得实数k的取值范围.
的最小值,再根据导数求g(x)单调性,由单调性确定其最小值取法,即得实数k的取值范围.
试题解析:(1)解 ∵f(x)=ex-x2+a,
∴f'(x)=ex-2x.
由已知,得![]()
解得![]()
∴函数f(x)的解析式为f(x)=ex-x2-1.
(2)证明 令φ(x)=f(x)+x2-x=ex-x-1,则φ'(x)=ex-1.
由φ'(x)=0,得x=0.
当x∈(-∞,0)时,φ'(x)<0,φ(x)单调递减;
当x∈(0,+∞)时,φ'(x)>0,φ(x)单调递增.
故φ(x)min=φ(0)=0,从而f(x)≥-x2+x.
(3)解 f(x)>kx对任意的x∈(0,+∞)恒成立![]() >k对任意的x∈(0,+∞)恒成立.
>k对任意的x∈(0,+∞)恒成立.
令g(x)=![]() ,x>0,
,x>0,
则g'(x)=![]()
=![]()
=![]() .
.
由(2)可知当x∈(0,+∞)时,ex-x-1>0恒成立,
由g'(x)>0,得x>1;由g'(x)<0,得0<x<1.
故g(x)的递增区间为(1,+∞),递减区间为(0,1),即g(x)min=g(1)=e-2.
故k<g(x)min=g(1)=e-2,即实数k的取值范围为(-∞,e-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
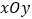 中,曲线
中,曲线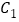 的参数方程为
的参数方程为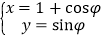 (其中
(其中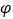 为参数),曲线
为参数),曲线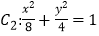 .以原点
.以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
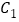 、
、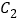 的极坐标方程;
的极坐标方程;(2)射线
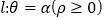 与曲线
与曲线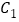 、
、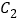 分别交于点
分别交于点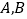 (且
(且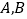 均异于原点
均异于原点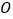 )当
)当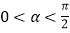 时,求
时,求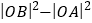 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex-1-x-ax2.
(1)若a=0,求f(x)的单调区间;
(2)若当x≥0时,f(x)≥0,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=x+b与函数f(x)=ln x的图象交于两个不同的点A,B,其横坐标分别为x1,x2,且x1<x2.
(1)求b的取值范围;
(2)当x2≥2时,证明x1·
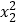 <2.
<2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f'(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b2>3a;
(3)若f(x),f'(x)这两个函数的所有极值之和不小于-
 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:
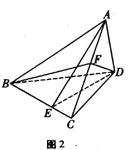
查看答案和解析>>【题目】如图2,在三棱锥A-BCD中,AB=CD=4, AC=BC=AD=BD=3.
(I)证明:AB
 CD;
CD;(II) E在线段BC上,BE=2EC, F是线段AC的中点,求平面ADE与平面BFD所成锐二面角的余弦值
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,F(-1, 0)是椭圆
 的左焦点,过点F且方向向量为
的左焦点,过点F且方向向量为 的光线,经直线
的光线,经直线 反射后通过左顶点D
反射后通过左顶点D .
.(I)求椭圆
 的方程;
的方程;(II)过点F作斜率为
 的直线
的直线 交椭圆
交椭圆 于A, B两点,M为AB的中点,直线OM (0为原点)与直线
于A, B两点,M为AB的中点,直线OM (0为原点)与直线 交于点P,若满足
交于点P,若满足 ,求
,求 的值.
的值.
相关试题

