【题目】已知0<α< ![]() <β<π,tan
<β<π,tan ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() .
.
(1)求sinα的值;
(2)求sinβ的值.
参考答案:
【答案】
(1)解:tanα= ![]() =
= ![]() ,
,
所以 ![]() =
= ![]() .
.
又因为sin2α+cos2α=1,
解得sin α= ![]() .
.
(2)解:因为0<α< ![]() <β<π,
<β<π,
所以0<β﹣α<π.
因为cos(β﹣α)= ![]() ,
,
所以sin(β﹣α)= ![]() .
.
因为0<α< ![]() ,sin α=
,sin α= ![]() .
.
所以cos α= ![]() ,
,
所以sin β=sin[(β﹣α)+α],
=sin(β﹣α)cos α+cos(β﹣α)sin α,
= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)根据二倍角公式和同角的三角函数的关系即可求出,(2)根据同角的三角函数的关系和两角和的正弦公式即可求出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
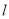 的参数方程为
的参数方程为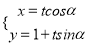 (
(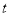 为参数,
为参数,  ),以坐标原点为极点,
),以坐标原点为极点, 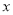 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为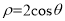 .
.(Ⅰ)讨论直线
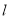 与圆
与圆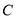 的公共点个数;
的公共点个数;(Ⅱ)过极点作直线
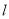 的垂线,垂足为
的垂线,垂足为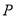 ,求点
,求点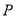 的轨迹与圆
的轨迹与圆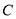 相交所得弦长.
相交所得弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|cosx|sinx,给出下列四个说法:
①f(x)为奇函数; ②f(x)的一条对称轴为x= ;
;
③f(x)的最小正周期为π; ④f(x)在区间[﹣ ,
,  ]上单调递增;
]上单调递增;
⑤f(x)的图象关于点(﹣ ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
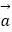 =(1,2),
=(1,2), 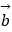 =(2,﹣2).
=(2,﹣2).
(1)设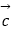 =4
=4 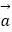 +
+ 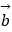 ,求
,求 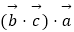 ;
;
(2)若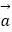 +
+ 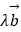 与
与 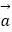 垂直,求λ的值;
垂直,求λ的值;
(3)求向量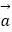 在
在 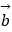 方向上的投影.
方向上的投影. -
科目: 来源: 题型:
查看答案和解析>>【题目】若动点
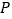 在直线
在直线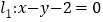 上,动点
上,动点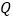 在直线
在直线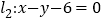 上,设线段
上,设线段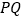 的中点为
的中点为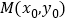 ,且
,且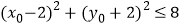 ,则
,则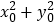 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sin2(
 +x)﹣
+x)﹣ 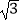 cos2x,
cos2x,
(1)求f(x)的最小正周期及单调递减区间;
(2)当x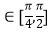 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
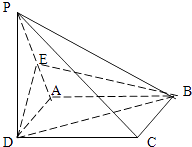
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
相关试题

