【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x,
cos2x,
(1)求f(x)的最小正周期及单调递减区间;
(2)当x ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
参考答案:
【答案】
(1)解:∵f(x)=[1﹣cos( ![]() +2x)]﹣
+2x)]﹣ ![]() cos2x
cos2x
=1+sin2x﹣ ![]() cos2x
cos2x
=1+2sin(2x﹣ ![]() )
)
∴最小正周期T=π
由 ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈Z
+2kπ,k∈Z
得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z
+kπ,k∈Z
∴单调递减区间为[ ![]() +kπ,
+kπ, ![]() +kπ]k∈Z
+kπ]k∈Z
(2)解:∵x∈[ ![]() ,
, ![]() ],
],
∴ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,
,
即2≤1+2sin(2x﹣ ![]() )≤3,
)≤3,
∴f(x)max=3,f(x)min=2.
【解析】(1)由两角和与差的正弦函数将f(x)=[1﹣cos( ![]() +2x)]﹣
+2x)]﹣ ![]() cos2x化为f(x)=1+2sin(2x﹣
cos2x化为f(x)=1+2sin(2x﹣ ![]() ),利用正弦函数的性质即可求f(x)的最小正周期及单调递减区间;(2)由x∈[
),利用正弦函数的性质即可求f(x)的最小正周期及单调递减区间;(2)由x∈[ ![]() ,
, ![]() ],可求得2x﹣
],可求得2x﹣ ![]() 的范围,从而可得f(x)的最大值和最小值.
的范围,从而可得f(x)的最大值和最小值.
【考点精析】本题主要考查了两角和与差的正弦公式和二倍角的余弦公式的相关知识点,需要掌握两角和与差的正弦公式:![]() ;二倍角的余弦公式:
;二倍角的余弦公式:![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
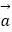 =(1,2),
=(1,2), 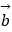 =(2,﹣2).
=(2,﹣2).
(1)设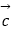 =4
=4 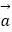 +
+ 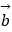 ,求
,求 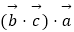 ;
;
(2)若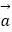 +
+ 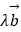 与
与 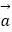 垂直,求λ的值;
垂直,求λ的值;
(3)求向量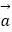 在
在 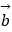 方向上的投影.
方向上的投影. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知0<α<
 <β<π,tan
<β<π,tan  ,cos(β﹣α)=
,cos(β﹣α)= 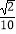 .
.
(1)求sinα的值;
(2)求sinβ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若动点
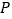 在直线
在直线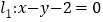 上,动点
上,动点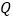 在直线
在直线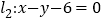 上,设线段
上,设线段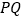 的中点为
的中点为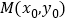 ,且
,且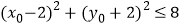 ,则
,则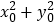 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
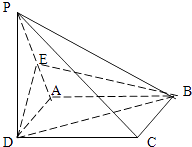
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)当
 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①
 ,②
,②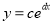 拟合,得到回归方程分别为
拟合,得到回归方程分别为 ,
, 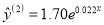 ,作残差分析,如表:
,作残差分析,如表:身高
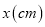
60
70
80
90
100
110
体重
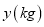
6
8
10
14
15
18
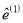
0.41
0.01
1.21
-0.19
0.41
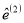
-0.36
0.07
0.12
1.69
-0.34
-1.12
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于
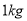 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.(结果保留到小数点后两位)
附:对于一组数据
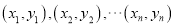 ,其回归直线
,其回归直线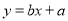 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为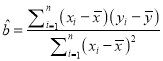 ,
, 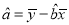 .
.
相关试题

