【题目】“糖尿病”已经成为日渐多发的一种疾病,其具有危害性大且难以完全治愈的特征.为了更好的抑制“糖尿病”多发的势头,某社区卫生医疗机构针对所服务居民开展了免费测血糖活动,将随机抽取的10名居民均分为![]() ,
, ![]() 两组(
两组(![]() 组:4.3,5.1,4.6,4.1,4.9;
组:4.3,5.1,4.6,4.1,4.9; ![]() 组:5.1,4.9,4.0,4.0,4.5).
组:5.1,4.9,4.0,4.0,4.5).
(1)通过提供的数据请判断哪一组居民的血糖值更低;
(2)现从![]() 组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
参考答案:
【答案】(1) ![]() 组居民的血糖值更低(2)
组居民的血糖值更低(2) ![]()
【解析】试题分析: (1)根据题中给出的数据分别计算A,B两组的平均数,比较可得结果;(2) 从![]() 组5名居民中随机选取2名,基本事件总数为10,这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,列举出基本事件,根据古典概型求出概率,再求出事件的对立事件即可.
组5名居民中随机选取2名,基本事件总数为10,这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,列举出基本事件,根据古典概型求出概率,再求出事件的对立事件即可.
试题解析:
(1)![]() 组5名居民血糖值的平均数
组5名居民血糖值的平均数![]() ,
,
![]() 组5名居民血糖值的平均数
组5名居民血糖值的平均数![]() ,
,
从计算结果看, ![]() 组居民的血糖值更低.
组居民的血糖值更低.
(2)从![]() 组5名居民中随机选取2名,基本事件总数为10,
组5名居民中随机选取2名,基本事件总数为10,
这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,这2名居民的血糖值都不低于4.5,包含的基本事件有![]() ,
, ![]() ,
, ![]() ,
,
所以这2名居民的血糖值都不低于4.5的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是递增的等差数列a3=
 ,且a2a4=6.
,且a2a4=6.
(1)求{an}的首项a1和公差d;
(2)求{an}的通项和前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的方程为x=﹣2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
(1)过M点的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的 ,求直线l1的方程;
,求直线l1的方程;
(2)若椭圆中a,c满足 =2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
=2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
(3)过M点作直线l2与圆相切于点N,设(2)中椭圆的两个焦点分别为F1 , F2 , 求三角形△NF1F2面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
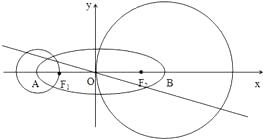
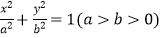 ,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线
,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线 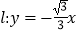 被圆A和圆B截得的弦长之比为
被圆A和圆B截得的弦长之比为 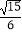 ;
; 
(1)求椭圆C的离心率;
(2)己知a=7,问是否存在点P,使得过P点有无数条直线被圆A和圆B截得的弦长之比为 ;若存在,请求出所有的P点坐标;若不存在,请说明理由.
;若存在,请求出所有的P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
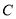
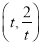 (
(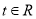 ,且
,且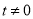 )为圆心的圆与
)为圆心的圆与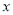 轴交于点
轴交于点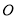 ,
, 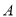 ,与
,与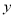 轴交于点
轴交于点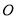 ,
, 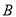 ,其中
,其中 为坐标原点.
为坐标原点.(1)求证:
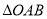 的面积为定值;
的面积为定值;(2)设直线
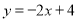 与圆
与圆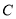 交于点
交于点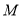 ,
, 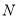 ,若
,若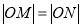 ,求圆
,求圆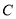 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x,y)在双曲线
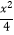 ﹣y2=1上,则3x2﹣2xy的最小值是 .
﹣y2=1上,则3x2﹣2xy的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA=
 ,c=3b,且△ABC面积S△ABC=
,c=3b,且△ABC面积S△ABC= 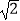 .
.
(1)求边b.c;
(2)求边a并判断△ABC的形状.
相关试题

