【题目】某县教育局为了检查本县甲、乙两所学校的学生对安全知识的学习情况,在这两所学校进行了安全知识测试,随机在这两所学校各抽取20名学生的考试成绩作为样本,成绩大于或等于80分的为优秀,否则为不优秀,统计结果如下图:


甲校 乙校
(1)从乙校成绩优秀的学生中任选两名,求这两名学生的成绩恰有一个落在![]() 内的概率;
内的概率;
(2)由以上数据完成下面列联表,并回答能否在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关。
甲校 | 乙校 | 总计 | |
优秀 | |||
不优秀 | |||
总计 |
![]()
参考数据 | P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1) ![]() .
.
(2)列联表见解析;在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关.
【解析】分析:(1)根据频率和为![]() ,求得
,求得![]() 的值,再计算乙校成绩优秀的学生数,利用列举法求出从乙校成绩优秀的学生中任选两名的基本事件的总数为
的值,再计算乙校成绩优秀的学生数,利用列举法求出从乙校成绩优秀的学生中任选两名的基本事件的总数为![]() ,两名学生的成绩恰有一个落在
,两名学生的成绩恰有一个落在![]() 内的基本事件的个数为
内的基本事件的个数为![]() ,利用古典概型概率公式可得结果. (2)根据列联表中数据,利用公式
,利用古典概型概率公式可得结果. (2)根据列联表中数据,利用公式![]() 求得
求得![]() ,从而可得结果.
,从而可得结果.
详解:(1)∵频率分布直方图中矩形面积为1
![]()
![]()
成绩落在![]() 内的人数为
内的人数为![]()
成绩落在![]() 内的人数为
内的人数为![]()
从乙校成绩优秀的学生中任选两名的基本事件的总数为![]()
两名学生的成绩恰有一个落在![]() 内的基本事件的个数为
内的基本事件的个数为![]()
则这两名学生的成绩恰有一个落在![]() 内的概率为:
内的概率为:![]()
(2)由已知得列联表如下
甲校 | 乙校 | 总计 | |
优秀 | 11 | 5 | 16 |
不优秀 | 9 | 15 | 24 |
总计 | 20 | 20 | 40 |
![]()
![]()
![]()
![]() 所以在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关.
所以在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
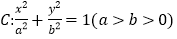 的离心率为
的离心率为 ,
,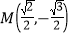 是椭圆上一点.
是椭圆上一点.(1)求椭圆的标准方程;
(2)过椭圆右焦点
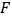 的直线与椭圆交于
的直线与椭圆交于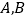 两点,
两点,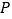 是直线
是直线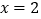 上任意一点.证明:直线
上任意一点.证明:直线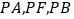 的斜率成等差数列.
的斜率成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程
 ,其中
,其中 ,
, .
.(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各
 名,将男性、女性使用微信的时间分成
名,将男性、女性使用微信的时间分成 组:
组: ,
, ,
, ,
, ,
, 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图. 
(1)根据女性频率分布直方图,估计女性使用微信的平均时间;
(2)若每天玩微信超过
 小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成
小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成 的列联表,并判断是否有
的列联表,并判断是否有 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?参考公式:
 ,其中
,其中 .
.参考数据:

-
科目: 来源: 题型:
查看答案和解析>>【题目】从高三抽出
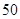 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求: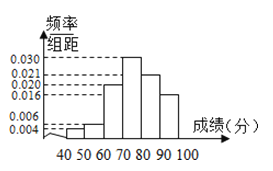
(1)这
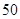 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;(2)这
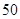 名学生的平均成绩.
名学生的平均成绩. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中ω>0),若f(x)的一条对称轴离最近的对称中心的距离为
(其中ω>0),若f(x)的一条对称轴离最近的对称中心的距离为  .
.
(1)求y=f(x)的单调递增区间;
(2)在△ABC中角A、B、C的对边分别是a,b,c满足(2b﹣a)cosC=ccosA,则f(B)恰是f(x)的最大值,试判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对
 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
相关试题

