【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,
两点,![]() 是直线
是直线![]() 上任意一点.证明:直线
上任意一点.证明:直线![]() 的斜率成等差数列.
的斜率成等差数列.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】分析:(1)由椭圆的离心率为![]() ,以及点M在椭圆上,结合a,b,c关系列出方程组求解即可;
,以及点M在椭圆上,结合a,b,c关系列出方程组求解即可;
(2)分过椭圆右焦点![]() 的直线斜率不存在和存在两种情况,进行整理即可.
的直线斜率不存在和存在两种情况,进行整理即可.
详解:(1)![]() ;
;

(2)因为右焦点![]() ,
,
当直线![]() 的斜率不存在时其方程为
的斜率不存在时其方程为![]() ,
,
因此,设![]() ,则
,则![]() ,
,
所以![]() 且
且![]() ,
,
所以,![]() ,
,
因此,直线![]() 和
和![]() 的斜率是成等差数列.
的斜率是成等差数列.
当直线![]() 的斜率存在时其方程设为
的斜率存在时其方程设为![]() ,
,
由 得,
得,![]() ,
,
所以![]() ,
,
因此,![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
所以,![]() ,
,
又因为![]() ,
,
所以有![]() ,
,
因此,直线![]() 和
和![]() 的斜率是成等差数列,
的斜率是成等差数列,
综上可知直线![]() 和
和![]() 的斜率是成等差数列.
的斜率是成等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图的算法框图,输出的结果S的值为( )

A.
B.0
C.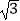
D.-
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b在区间
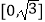 上取值,则函数
上取值,则函数 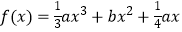 在R上有两个相异极值点的概率是( )
在R上有两个相异极值点的概率是( )
A.
B.1-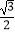
C.
D.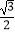
-
科目: 来源: 题型:
查看答案和解析>>【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是
 ,样本数据分组为
,样本数据分组为 .
.
(1)求直方图中
 的值;
的值;(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用
 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程
 ,其中
,其中 ,
, .
.(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各
 名,将男性、女性使用微信的时间分成
名,将男性、女性使用微信的时间分成 组:
组: ,
, ,
, ,
, ,
, 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图. 
(1)根据女性频率分布直方图,估计女性使用微信的平均时间;
(2)若每天玩微信超过
 小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成
小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成 的列联表,并判断是否有
的列联表,并判断是否有 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?参考公式:
 ,其中
,其中 .
.参考数据:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某县教育局为了检查本县甲、乙两所学校的学生对安全知识的学习情况,在这两所学校进行了安全知识测试,随机在这两所学校各抽取20名学生的考试成绩作为样本,成绩大于或等于80分的为优秀,否则为不优秀,统计结果如下图:


甲校 乙校
(1)从乙校成绩优秀的学生中任选两名,求这两名学生的成绩恰有一个落在
 内的概率;
内的概率;(2)由以上数据完成下面列联表,并回答能否在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关。
甲校
乙校
总计
优秀
不优秀
总计

参考数据
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
span>3.841
5.024
6.635
7.879
10.828
相关试题

