【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,都有
,都有![]() 成立.记
成立.记![]() .
.
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(I)由![]() 成立,可得
成立,可得![]() 时,
时, ![]() ,可得出数列
,可得出数列![]() 为等比数列,从而可得数列
为等比数列,从而可得数列![]() 的通项公式,根据对数的运算性质可得
的通项公式,根据对数的运算性质可得![]() ;(II)利用(I)的结论,可得
;(II)利用(I)的结论,可得![]() ,根据裂项求和求出数列
,根据裂项求和求出数列![]() 的前
的前![]() 项和为
项和为![]() ,再利用放缩法即可证明结论.
,再利用放缩法即可证明结论.
试题解析:(Ⅰ)在![]() 中,令
中,令![]() 得
得![]() .
.
因为对任意正整数![]() ,都有
,都有![]() 成立,
成立, ![]() 时,
时, ![]() ,
,
两式作差得, ![]() ,所以
,所以![]() ,
,
又![]() ,所以数列
,所以数列![]() 是以
是以![]() 为首项,4为公比的等比数列,即
为首项,4为公比的等比数列,即![]() ,
,
∴![]()
(Ⅱ)∵![]() ,
,
∴![]() .
.
∴![]() .
.
![]()
![]()
∴对任意![]() ,
, ![]() .
.
又![]() ,所以,
,所以, ![]() 为关于
为关于![]() 的增函数,所以
的增函数,所以![]() ,
,
综上, ![]()
【方法点晴】本题主要考查等差数列的通项与等比数列的定义,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
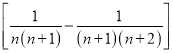 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=
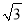 ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
 AD=1,CD=
AD=1,CD=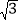 .
.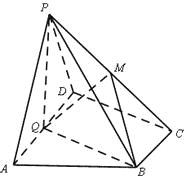
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
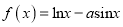 在区间
在区间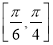 上是单调增函数,则实数
上是单调增函数,则实数 的取值范围为( )
的取值范围为( )A.
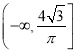 B.
B. 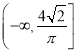 C.
C. 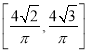 D.
D. 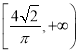
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 与等边
与等边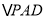 所在的平面相互垂直,
所在的平面相互垂直, 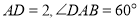 ,点E,F分别为PC和AB的中点.
,点E,F分别为PC和AB的中点.(Ⅰ)求证:EF∥平面PAD
(Ⅱ)证明:
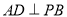 ;
;(Ⅲ)求三棱锥
 的体积.
的体积.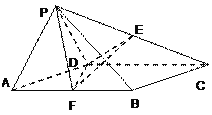
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
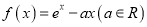 (
(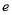 为自然对数的底数).
为自然对数的底数).(Ⅰ)讨论
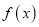 的单调性;
的单调性;(Ⅱ)若
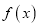 有两个零点
有两个零点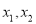 ,求
,求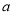 的取值范围;
的取值范围;(2)在(1)的条件下,求证:
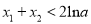 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
在直角坐标系
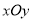 中,直线
中,直线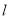 的参数方程为
的参数方程为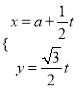
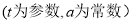 .以坐标原点为极点,以
.以坐标原点为极点,以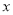 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线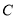 的极坐标方程为
的极坐标方程为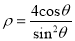 .
.(Ⅰ)写出
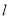 的普通方程和
的普通方程和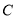 的直角坐标方程;
的直角坐标方程;(Ⅱ)设直线
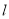 与曲线
与曲线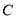 交于A,B两点,当
交于A,B两点,当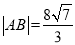 时,求
时,求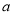 的值.
的值.
相关试题

