【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
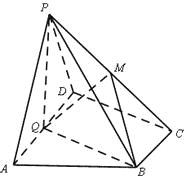
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
参考答案:
【答案】(1)∵AD //BC,BC=![]() AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,∴BQ⊥平面PAD.∵BQ
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,∴BQ⊥平面PAD.∵BQ![]() 平面PQB,∴平面PQB⊥平面PAD.
平面PQB,∴平面PQB⊥平面PAD.
(2)![]() .
.
【解析】试题分析:(1)∵AD //BC,BC=![]() AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.
又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ![]() 平面PQB,∴平面PQB⊥平面PAD.
平面PQB,∴平面PQB⊥平面PAD.
(2)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为![]() ;
;![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴ , ∴
, ∴
在平面MBQ中,![]() ,
,![]() ,
,
∴ 平面MBQ法向量为![]() .
.
∵二面角M-BQ-C为30,![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
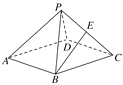
A. BE∥平面PAD,且BE到平面PAD的距离为
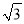
B. BE∥平面PAD,且BE到平面PAD的距离为

C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=
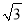 ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
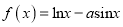 在区间
在区间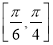 上是单调增函数,则实数
上是单调增函数,则实数 的取值范围为( )
的取值范围为( )A.
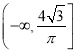 B.
B. 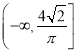 C.
C. 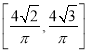 D.
D. 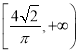
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
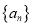 的前
的前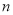 项和为
项和为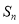 ,且对任意正整数
,且对任意正整数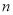 ,都有
,都有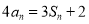 成立.记
成立.记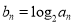 .
.(Ⅰ)求数列
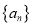 和
和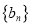 的通项公式;
的通项公式;(Ⅱ)设
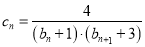 ,数列
,数列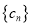 的前
的前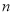 项和为
项和为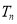 ,求证:
,求证: 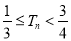 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 与等边
与等边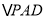 所在的平面相互垂直,
所在的平面相互垂直, 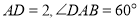 ,点E,F分别为PC和AB的中点.
,点E,F分别为PC和AB的中点.(Ⅰ)求证:EF∥平面PAD
(Ⅱ)证明:
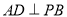 ;
;(Ⅲ)求三棱锥
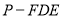 的体积.
的体积.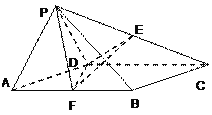
相关试题

