【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为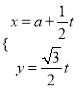
![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于A,B两点,当
交于A,B两点,当![]() 时,求
时,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】试题分析:(I)将直线![]() 的参数方程为
的参数方程为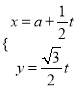 利用代入法消去参数即可得到
利用代入法消去参数即可得到![]() 的普通方程,由
的普通方程,由![]() 极坐标方程为
极坐标方程为![]() 得
得![]() ,利用互化公式可得
,利用互化公式可得![]() 的直角坐标方程;(Ⅱ)将直线
的直角坐标方程;(Ⅱ)将直线![]() 的参数方程代入
的参数方程代入![]() 的直角坐标方程,根据韦达定理以及直线参数方程的几何意义列方程求解即可.
的直角坐标方程,根据韦达定理以及直线参数方程的几何意义列方程求解即可.
试题解析:(Ⅰ)依题意由直线![]() :
: 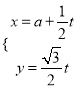 得
得![]() ,
,
即![]()
由![]() 极坐标方程为
极坐标方程为![]() 得
得![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]()
(Ⅱ)依题意,直线![]() 过点
过点![]() ,直线
,直线![]() 的参数方程与
的参数方程与![]() 的直角坐标方程联立
的直角坐标方程联立
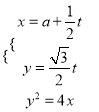 得
得![]() ,
, ![]()
∴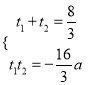 ,
,
∴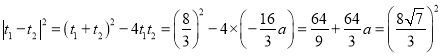 ;
;
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
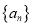 的前
的前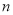 项和为
项和为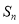 ,且对任意正整数
,且对任意正整数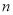 ,都有
,都有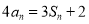 成立.记
成立.记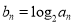 .
.(Ⅰ)求数列
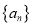 和
和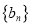 的通项公式;
的通项公式;(Ⅱ)设
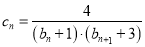 ,数列
,数列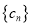 的前
的前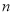 项和为
项和为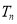 ,求证:
,求证: 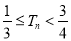 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 与等边
与等边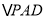 所在的平面相互垂直,
所在的平面相互垂直, 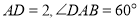 ,点E,F分别为PC和AB的中点.
,点E,F分别为PC和AB的中点.(Ⅰ)求证:EF∥平面PAD
(Ⅱ)证明:
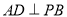 ;
;(Ⅲ)求三棱锥
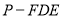 的体积.
的体积.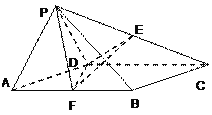
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
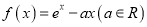 (
(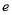 为自然对数的底数).
为自然对数的底数).(Ⅰ)讨论
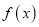 的单调性;
的单调性;(Ⅱ)若
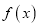 有两个零点
有两个零点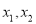 ,求
,求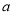 的取值范围;
的取值范围;(2)在(1)的条件下,求证:
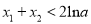 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别是a,b,c,且2acosA=bcosC+ccosB.
(Ⅰ)求A的大小;
(Ⅱ)若a=2,求b+c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点.

(Ⅰ)求证:PC∥平面EBD;
(Ⅱ)求证:平面PBC⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员x名.
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求x的值;
(Ⅱ)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择,求该客户最终聘请的家政服务员中既有A类又有B类的概率.
相关试题

