【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在实数p,q,r,对于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在说明理由.
参考答案:
【答案】
(1)解:设等差数列的公差为d,等比数列的公比为q,
由a1=b1=2,得a4=2+3d,b4=2q3,s4=8+6d,
由a4+b4=27,S4﹣b4=10得, ![]() ,
,
解得d=3,q=2,
所以an=3n﹣1,bn=2n
(2)解:假设存在实数p,q,r,对于任意n∈N*,都有Tn=pan+qbn+r,
由(1)得,Tn=anb1+an﹣1b2+…+a1bn
= ![]() ①
①
∴2Tn= ![]() ②
②
由②﹣①得,
Tn=﹣2(3n﹣1)+3×(22+23+…+2n)+2n+2
=3× ![]() +2n+2﹣6n+2
+2n+2﹣6n+2
=102n﹣6n﹣10
∴Tn=﹣2(3n﹣1)+10×2n﹣12=pan+qbn+r,
可得p=﹣2;q=10;r=﹣12,
即存在p=﹣2;q=10;r=﹣12满足条件
【解析】(1)设出首项和公差,根据等差、等比数列的通项公式和等差数列的前n项和公式,列出方程组求出首项和公差,即可求出an、bn;(2)假设存在实数p、q、r满足条件,由(1)表示出Tn , 利用错位相减法求出Tn的表达式化简后即可求出实数p、q、r的值.
【考点精析】认真审题,首先需要了解等差数列的通项公式(及其变式)(通项公式:![]() 或
或![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2﹣(a+2)x+2<0.
(1)当a=﹣1时,解不等式;
(2)当a∈R时,解不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数:f(x)=x2+bx+c,其中:0≤b≤4,0≤c≤4,记函数f(x)满足条件:
 的事件为A,则事件A发生的概率为( )
的事件为A,则事件A发生的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线ax﹣by+2=0(a>0,b>0)被圆x2+y2+4x﹣4y﹣1=0所截得的弦长为6,则
 的最小值为( )
的最小值为( )
A.10
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图给出的是计算
 的值的一个程序框图,判断框内应填入的条件是( )
的值的一个程序框图,判断框内应填入的条件是( ) 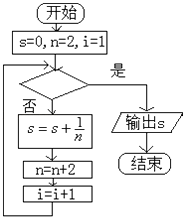
A.i<20
B.i>20
C.i<10
D.i>10 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1﹣|x|+
 ,若f(x﹣2)>f(3),则x的取值范围是
,若f(x﹣2)>f(3),则x的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
相关试题

