【题目】已知关于x的不等式ax2﹣(a+2)x+2<0.
(1)当a=﹣1时,解不等式;
(2)当a∈R时,解不等式.
参考答案:
【答案】
(1)解:当a=﹣1时,此不等式为﹣x2﹣x+2<0,
可化为x2+x﹣2>0,
化简得(x+2)(x﹣1)>0,
解得即{x|x<﹣2或x>1};
(2)解:不等式ax2﹣(a+2)x+2<0化为(ax﹣2)(x﹣1)<0,
当a=0时,x>1;
当a>0时,不等式化为(x﹣ ![]() )(x﹣1)<0,
)(x﹣1)<0,
若 ![]() <1,即a>2,解不等式得
<1,即a>2,解不等式得 ![]() <x<1;
<x<1;
若 ![]() =1,即a=2,解不等式得x∈;
=1,即a=2,解不等式得x∈;
若 ![]() >1,即0<a<2,解不等式得1<x<
>1,即0<a<2,解不等式得1<x< ![]() ;
;
当a<0时,不等式(x﹣ ![]() )(x﹣1)>0,解得x<
)(x﹣1)>0,解得x< ![]() 或x>1;
或x>1;
综上所述:当a=0,不等式的解集为{x|x>1};
当a<0时,不等式的解集为{x|x< ![]() 或x>1};
或x>1};
当0<a<2时,不等式的解集为{x|1<x< ![]() };
};
当a=2时,不等式的解集为;
当a>2时,不等式的解集为{x| ![]() <x<1}
<x<1}
【解析】(1)a=﹣1时,不等式化为﹣x2﹣x+2<0,求解即可;(2)不等式化为(ax﹣2)(x﹣1)<0,讨论a=0、a>0和a<0时,对应不等式的解集是什么,从而求出对应的解集.
【考点精析】掌握解一元二次不等式是解答本题的根本,需要知道求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
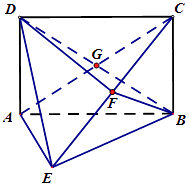
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)当
 时,若函数
时,若函数 的导函数
的导函数 的图象与
的图象与 轴交于
轴交于 ,
,  两点,其横坐标分别为
两点,其横坐标分别为 ,
,  ,线段
,线段 的中点的横坐标为
的中点的横坐标为 ,且
,且 ,
,  恰为函数
恰为函数 的零点,求证:
的零点,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆 交于
交于 ,
,  两点.
两点.(1)求圆
 的直角坐标方程及弦
的直角坐标方程及弦 的长;
的长;(2)动点
 在圆
在圆 上(不与
上(不与 ,
,  重合),试求
重合),试求 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数:f(x)=x2+bx+c,其中:0≤b≤4,0≤c≤4,记函数f(x)满足条件:
 的事件为A,则事件A发生的概率为( )
的事件为A,则事件A发生的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线ax﹣by+2=0(a>0,b>0)被圆x2+y2+4x﹣4y﹣1=0所截得的弦长为6,则
 的最小值为( )
的最小值为( )
A.10
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在实数p,q,r,对于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在说明理由.
相关试题

