【题目】如图所示,平面ABC⊥平面BCDE,BC∥DE, ![]() ,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.
,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点. 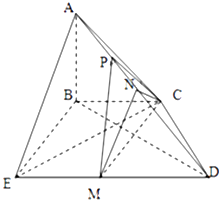
(1)证明:平面MNC⊥平面BCDE;
(2)若EC⊥CD,点P为棱AD的三等分点(近A),平面PMC与平面ABC所成锐二面角的余弦值为 ![]() ,求棱AB的长度.
,求棱AB的长度.
参考答案:
【答案】
(1)证明:连结BM,ON,
由题意四边形BMDC是菱形,∴O是BD中点,
∵N是AD中点,∴ON∥AB,
∵AB⊥BC,平面ABC⊥平面BCDE,∴AB⊥平面BCDE,
∴ON⊥平面BCDE,
∵ON平面MNC,∴平面MNC⊥平面BCDE
(2)解:以C为原点,CE为x轴,CD为y轴,过C作平面BCDE的垂线为z轴,建立空间直角坐标系,
设A( ![]() ,﹣1,t),(t>0)由题意D(0,2,0),P(
,﹣1,t),(t>0)由题意D(0,2,0),P( ![]() ,0,
,0, ![]() ),E(2
),E(2 ![]() ,0,0),
,0,0),
D(0,2,0),M( ![]() ),B(
),B( ![]() ,0),C(0,0,0),
,0),C(0,0,0),
![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ),
), ![]() =(
=( ![]() ,0),
,0), ![]() =(
=( ![]() ),
),
设平面PMC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 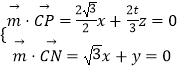 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ,﹣3,﹣
,﹣3,﹣ ![]() ),
),
设平面ABC的法向量 ![]() =(a,b,c),
=(a,b,c),
则 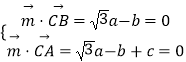 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ,0),
,0),
∵平面PMC与平面ABC所成锐二面角的余弦值为 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
= ![]() =
= ![]() ,解得t=3.
,解得t=3.
∴棱AB的长度为3.
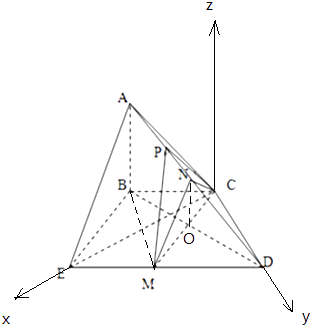
【解析】(1)连结BM,ON,推导出ON∥AB,AB⊥平面BCDE,从而ON⊥平面BCDE,由此能证明平面MNC⊥平面BCDE.(2)以C为原点,CE为x轴,CD为y轴,过C作平面BCDE的垂线为z轴,建立空间直角坐标系,利用向量法能求出棱AB的长度.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数f(x)=lg
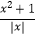 (x≠0,x∈R)有下列命题:
(x≠0,x∈R)有下列命题:
①函数y=f(x)的图象关于y轴对称;
②在区间(﹣∞,0)上,函数y=f(x)是减函数;
③函数f(x)的最小值为lg2;
④在区间(1,+∞)上,函数f(x)是增函数.
其中正确命题序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U={1,2,3,4},集合A={1,2,x2}与B={1,4}是它的子集,
(1)求UB;
(2)若A∩B=B,求x的值;
(3)若A∪B=U,求x. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
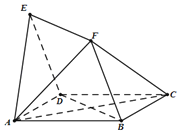
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若变量x,y满足约束条件
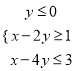 ,则z=3x+5y的取值范围是( )
,则z=3x+5y的取值范围是( )A. [3,+∞) B. [﹣8,3] C. (﹣∞,9] D. [﹣8,9]
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
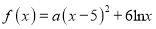 ,其中
,其中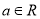 ,曲线
,曲线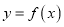 在点
在点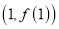 处的切线与
处的切线与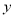 轴相交于点
轴相交于点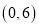 .
.(1)确定
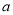 的值;
的值;(2)求函数
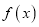 的单调区间与极值.
的单调区间与极值.
相关试题

