【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.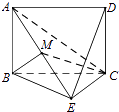
参考答案:
【答案】证明:(Ⅰ)因为平面ABCD⊥平面BEC,
所以AB⊥平面BEC,故AB⊥EC.
因为BE⊥EC,所以EC⊥平面ABE,
故EC⊥BM.
因为AB=BE,M为AE的中点,所以AE⊥BM.
所以BM⊥平面AEC.
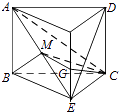
解:(Ⅱ)如图,将几何体ABCDE补成三棱柱AFD﹣BEC,
设EF的中点为G,连结MG,GC.
因为MG∥BE,所以MG⊥平面DEC.
因此∠MCG为MC与平面DEC所成的角.
不妨设AB=2,则AB=BE=EC=2,
因此MG=1, ![]() ,
, ![]() ,
,
故 ![]() ,
,
所以MC与平面DEC所成的角的余弦值为 ![]() .
.
【解析】(Ⅰ)由已知推导出AB⊥EC,EC⊥BM,AE⊥BM,由此能证明BM⊥平面AEC.(Ⅱ)将几何体ABCDE补成三棱柱AFD﹣BEC,设EF的中点为G,连结MG,GC,推导出∠MCG为MC与平面DEC所成的角,由此能求出MC与平面DEC所成的角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则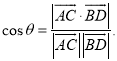 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,AB=AC=2PA=2,∠PAB=∠PAC=∠BAC=
 .
.
(Ⅰ) 证明:AP⊥BC;
(Ⅱ)求三棱锥P﹣ABC的体积.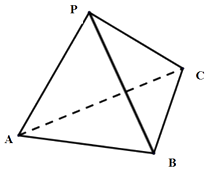
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.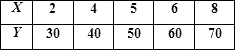
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;(2)曲线
 与
与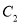 相交于
相交于 两点,求过
两点,求过 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0 , 使f(x0)≤0的概率是( )
A.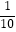
B.
C.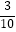
D.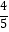
相关试题

