【题目】如图,在三棱锥P﹣ABC中,AB=AC=2PA=2,∠PAB=∠PAC=∠BAC= ![]() .
.
(Ⅰ) 证明:AP⊥BC;
(Ⅱ)求三棱锥P﹣ABC的体积.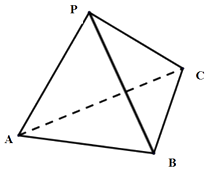
参考答案:
【答案】(Ⅰ)证明:由已知可得 ![]() ,
,
由余弦定理得 ![]() ,则AB2=PB2+AP2 ,
,则AB2=PB2+AP2 ,
∴AP⊥PB,同理AP⊥PC,又PB∩PC=P.
∴AP⊥平面PBC,则AP⊥BC;
(Ⅱ) 解:在Rt△APB中,由AB=2PA=2,得PB= ![]() ,
,
同理求得PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,∴BC=2,
,∴BC=2,
∴△PBC边BC上的高为 ![]() ,
,
则 ![]() .
.
∵VP﹣ABC=VA﹣PBC ,
∴ ![]()
【解析】(Ⅰ)由已知结合余弦定理求得PB、PC的长度,可得AP⊥PB,AP⊥PC,再由线面垂直的判定可得AP⊥平面PBC,则AP⊥BC;(Ⅱ)求解直角三角形可得PB=PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,得BC=2,进一步求出△PBC边BC上的高,得到
,得BC=2,进一步求出△PBC边BC上的高,得到 ![]() .结合VP﹣ABC=VA﹣PBC可得
.结合VP﹣ABC=VA﹣PBC可得
三棱锥P﹣ABC的体积.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
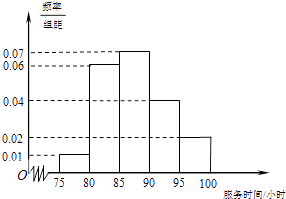
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.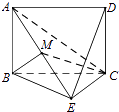
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.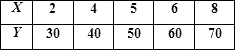
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
相关试题

