【题目】函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0 , 使f(x0)≤0的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:∵f(x)≤0x2﹣x﹣2≤0﹣1≤x≤2,
∴f(x0)≤0﹣1≤x0≤2,即x0∈[﹣1,2],
∵在定义域内任取一点x0 ,
∴x0∈[﹣5,5],
∴使f(x0)≤0的概率P= ![]() =
= ![]()
故选C
【考点精析】本题主要考查了解一元二次不等式和几何概型的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.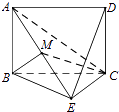
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.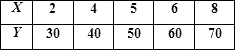
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;(2)曲线
 与
与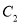 相交于
相交于 两点,求过
两点,求过 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知动点
中,已知动点 到定点
到定点 的距离与到定直线
的距离与到定直线 的距离之比为
的距离之比为 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)已知
 为定直线
为定直线 上一点.
上一点.①过点
 作
作 的垂线交轨迹
的垂线交轨迹 于点
于点 (
( 不在
不在 轴上),求证:直线
轴上),求证:直线 与
与 的斜率之积是定值;
的斜率之积是定值;②若点
 的坐标为
的坐标为 ,过点
,过点 作动直线
作动直线 交轨迹
交轨迹 于不同两点
于不同两点 ,线段
,线段 上的点
上的点 满足
满足 ,求证:点
,求证:点 恒在一条定直线上.
恒在一条定直线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,点
中,点 ,直线
,直线 与动直线
与动直线 的交点为
的交点为 ,线段
,线段 的中垂线与动直线
的中垂线与动直线 的交点为
的交点为 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过动点
 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,
,  ,求证:
,求证:  的大小为定值.
的大小为定值.
相关试题

