【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
参考答案:
【答案】(1)![]() ;(2)12名;(3)
;(2)12名;(3)![]()
【解析】
试题(1)先根据抽到初二年级女生的概率是0.19,做出初二女生的人数;(2)再用全校的人数减去初一和初二的人数,得到初三的人数,全校要抽取48人,做出每个个体被抽到的概率,做出初三被抽到的人数;(3)由题意,y+z=500,y≥245,z≥245,即可求出初三年级中女生比男生多的概率
试题解析:(1)因为![]() ,所以
,所以![]()
(2)初三年级人数为![]()
应在初三年级抽取![]() 人
人
(3)设初三年级女生比男生多的事件为A,初三年级女生、男生数记为(y,z),
由(2)知y+z=500,且y、z为正整数.
基本事件有(245,255),(246,254),(247,253),…,(255,245)共11个,
事件A包含的基本事件有(251,249),(252,248),(253,247),(254,246),(255,245)共5个,
所以P(A)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组
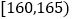 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 也为抛物线
也为抛物线 的焦点.(1)若
的焦点.(1)若 为椭圆
为椭圆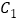 上两点,且线段
上两点,且线段 的中点为
的中点为 ,求直线
,求直线 的斜率;
的斜率;(2)若过椭圆
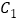 的右焦点
的右焦点 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于 和
和 ,设线段
,设线段 的长分别为
的长分别为 ,证明
,证明 是定值.
是定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次新高考质量测评,在成绩统计分析中,某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
5
6
8
6
2
3
3
5
6
8
9
7
1
2
2
3
4
5
6
7
8
9
8
9
5
8

(1)求该班数学成绩在
 的频率及全班人数;
的频率及全班人数;(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定90分及其以上为优秀,现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况,求在抽取的2份试卷中至少有1份优秀的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 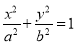 (
( )的离心率
)的离心率 ,直线
,直线 被以椭圆
被以椭圆 的短轴为直径的圆截得的弦长为
的短轴为直径的圆截得的弦长为 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 的直线
的直线 交椭圆于
交椭圆于 ,
,  两个不同的点,且
两个不同的点,且 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
, ,
, ,
, 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
 或
或 作品获得一等奖”;
作品获得一等奖”;乙说:“
 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
, 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
相关试题

