【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)函数![]() 的图象在点
的图象在点![]() 处的切线与函数
处的切线与函数![]() 的图象相切,求实数
的图象相切,求实数![]() 的值;
的值;
(2)若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,且
,且![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析: (1)求出函数![]() 的图象在点
的图象在点![]() 的切线方程,再由直线与抛物线相切,
的切线方程,再由直线与抛物线相切, ![]() ,求出实数
,求出实数![]() 的值; (2)由题意构造函数
的值; (2)由题意构造函数![]() ,求出
,求出![]() ,
, ![]() 在
在![]() 上有解,再由二次函数相关知识求出
上有解,再由二次函数相关知识求出![]() 的范围; (3)假定
的范围; (3)假定![]() ,先分别求出函数
,先分别求出函数![]() 在
在![]() 上的单调性,将原不等式转化为
上的单调性,将原不等式转化为![]() ,即
,即![]() 在
在![]() 上为增函数,求出实数
上为增函数,求出实数![]() 的范围.
的范围.
试题解析:(1)因为![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,
,
由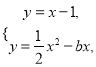 得
得![]() .
.
由![]() ,得
,得![]() .
.
(还可以通过导数来求![]() )
)
(2)因为![]()
![]()
![]() ,
,
所以![]() ,
,
由题意知![]() 在
在![]() 上有解,
上有解,
因为![]() ,设
,设![]() ,因为
,因为![]() ,
,
则只要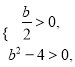 解得
解得![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
(3)不妨设![]() ,
,
因为函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
所以![]() ,
,
函数![]() 图象的对称轴为
图象的对称轴为![]() ,且
,且![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,
所以![]() ,
,
所以![]() ,
,
等价于![]() ,
,
即![]() ,
,
等价于![]()
![]() 在区间
在区间![]() 上是增函数,
上是增函数,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
等价于![]() 在区间
在区间![]() 上恒成立,所以
上恒成立,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
点睛: 本题主要考查导数的应用,包括导数的几何意义,导数与单调性,属于中档题.本题在第3问中注意解题思想:等价转换,将原不等式转化为求![]() 在
在![]() 上为增函数,等价于
上为增函数,等价于![]() 在区间
在区间![]() 上恒成立,分离出
上恒成立,分离出![]() ,转化为求
,转化为求![]() 在
在![]() 上的最小值.
上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机
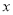 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为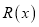 万元,且
万元,且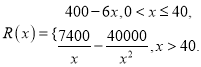
(1)写出年利润
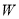 (万元)关于年产量
(万元)关于年产量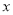 (万只)的函数解析式;
(万只)的函数解析式;(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人想参加《中国诗词大会》比赛,筹办方要从10首诗司中分别抽出3首让甲、乙背诵,规定至少背出其中2首才算合格; 在这10首诗词中,甲只能背出其中的7首,乙只能背出其中的8首
(1)求抽到甲能背诵的诗词的数量
 的分布列及数学期望;
的分布列及数学期望;(2)求甲、乙两人中至少且有一人能合格的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC中,内角A,B,C的对边分别为a,b,c,已知
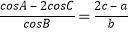
(1)求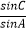 的值;
的值;
(2)若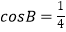 ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
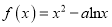 (
(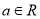 ),
),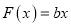 (
(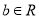 ).
).(1)讨论
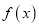 的单调性;
的单调性;(2)设
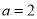 ,
, 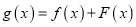 ,若
,若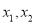 (
(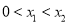 )是
)是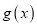 的两个零点,且
的两个零点,且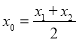 ,
,试问曲线
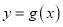 在点
在点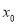 处的切线能否与
处的切线能否与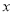 轴平行?请说明理由.
轴平行?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
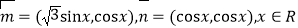 ,设
,设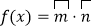 .
.(1)求函数
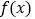 的解析式及单调递增区间;
的解析式及单调递增区间;(2)在
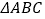 中,
中,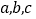 分别为内角
分别为内角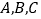 的对边,且
的对边,且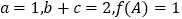 ,求
,求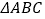 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Sn是正项数列{an}的前n项和,且Sn=
 an2+
an2+  an﹣
an﹣ 
(1)求数列{an}的通项公式;
(2)若an=2nbn , 求数列{bn}的前n项和.
相关试题

