【题目】如图,![]() 是底面边长为2,高为
是底面边长为2,高为![]() 的正三棱柱,经过AB的截面与上底面相交于PQ, 设
的正三棱柱,经过AB的截面与上底面相交于PQ, 设![]() .
.
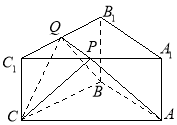
(Ⅰ)证明:![]() ;
;
(Ⅱ)当![]() 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离.
参考答案:
【答案】(Ⅰ) (Ⅱ)见解析
【解析】
试题分析:(I)由平面![]() ,利用线面平行的性质定理可得:
,利用线面平行的性质定理可得:![]() ,又
,又![]() ,即可证明
,即可证明![]() .(II)连结
.(II)连结![]() ,点
,点![]() 到平面
到平面![]() 的距离等于三棱锥
的距离等于三棱锥![]() 的高,设其值为
的高,设其值为![]() ,
,
当![]() 时,
时,![]() ,四边形
,四边形![]() 是等腰梯形,经计算得梯形的高为
是等腰梯形,经计算得梯形的高为![]() ,由此计算出
,由此计算出![]() ,
,![]() ,然后再根据
,然后再根据![]() ,可得
,可得![]() ,由此即可求出结果.
,由此即可求出结果.
试题解析: (Ⅰ)证明:∵ ![]() 是正三棱柱,
是正三棱柱,
∴平面![]() //平面
//平面![]() ……2分
……2分
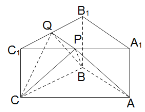
∵平面![]() 平面
平面![]() =
=![]() ,平面
,平面![]() 平面
平面![]() =
=![]()
∴![]()
∵![]() , ∴
, ∴![]()
(Ⅱ)连结![]() ,点
,点![]() 到平面
到平面![]() 的距离等于三棱锥
的距离等于三棱锥![]() 的高,设其值为
的高,设其值为![]()
当![]() 时,
时,![]() ,四边形
,四边形![]() 是等腰梯形,经计算得梯形的高为
是等腰梯形,经计算得梯形的高为![]()
∴![]() ,
,![]()
∵![]() 是正三棱柱,∴
是正三棱柱,∴![]()
得到![]()
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:

(1) 算出线性回归方程
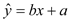 ; (a,b精确到十分位)
; (a,b精确到十分位)(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式:
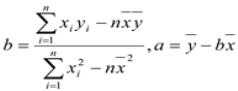 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
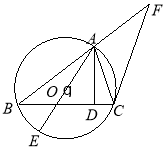
如图,已知圆
 是
是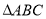 的外接圆,
的外接圆, 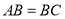 ,
,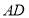 是
是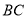 边上的高,
边上的高,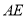 是圆
是圆 的直径,过点
的直径,过点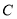 作圆
作圆 的切线交
的切线交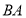 的延长线于点
的延长线于点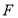 .
.
(Ⅰ)求证:
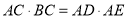 ;
; (Ⅱ)若
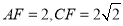 ,求
,求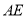 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
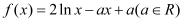 .
.(Ⅰ)讨论
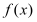 的单调性;
的单调性;(Ⅱ)若
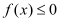 恒成立,证明:当
恒成立,证明:当 时,
时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】条件
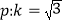 ;条件
;条件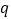 :直线
:直线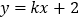 与圆
与圆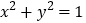 相切,则
相切,则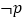 是
是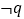 的( )
的( )A. 充分必要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
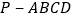 的底面
的底面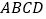 为正方形,
为正方形,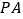 ⊥底面
⊥底面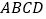 ,
,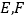 分别是
分别是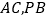 的中点,
的中点,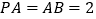 .
.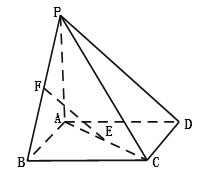
(Ⅰ)求证
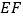 ∥平面
∥平面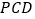 ;
;(Ⅱ)求直线
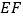 与平面
与平面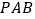 所成的角;
所成的角;(Ⅲ)求四棱锥
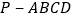 的外接球的体积.
的外接球的体积.
相关试题

