【题目】选修4—1:几何证明选讲
如图,已知圆![]() 是
是![]() 的外接圆,
的外接圆, ![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 作圆
作圆![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
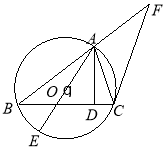
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)详见解析;(2) ![]()
【解析】
试题分析:(I)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E与∠ACB都是弧AB所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(II)利用切割线定理可得![]() ,可得BF.再利用△AFC∽△CFB,可得
,可得BF.再利用△AFC∽△CFB,可得![]() ,进而根据sin∠ACD=sin∠AEB,
,进而根据sin∠ACD=sin∠AEB,![]() ,即可得出答案.
,即可得出答案.
试题解析: (Ⅰ)证明:连结![]() ,由题意知
,由题意知![]() 为直角三角形
为直角三角形
因为![]() ,
,![]() ,
,![]()
所以![]()
即![]()
又![]() ,所以
,所以![]()
(Ⅱ)因为![]() 是圆
是圆![]() 的切线,所以
的切线,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]()
所以![]() ,得
,得![]() ,
,![]()
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年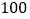 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照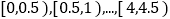 分成
分成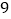 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.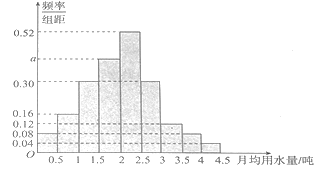
(1)求直方图中
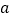 的值;
的值;(2)若该市有
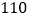 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于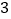 吨的人数,并说明理由;
吨的人数,并说明理由;(3)若该市政府希望使
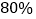 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准 (吨),估计
(吨),估计 的值(精确到
的值(精确到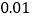 ),并说明理由.
),并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:

(1) 算出线性回归方程
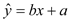 ; (a,b精确到十分位)
; (a,b精确到十分位)(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式:
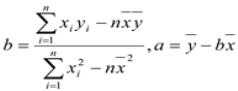 )
) -
科目: 来源: 题型:
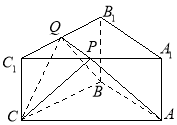
查看答案和解析>>【题目】如图,
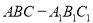 是底面边长为2,高为
是底面边长为2,高为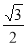 的正三棱柱,经过AB的截面与上底面相交于PQ, 设
的正三棱柱,经过AB的截面与上底面相交于PQ, 设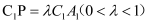 .
.
(Ⅰ)证明:
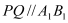 ;
; (Ⅱ)当
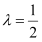 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
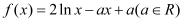 .
.(Ⅰ)讨论
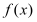 的单调性;
的单调性;(Ⅱ)若
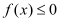 恒成立,证明:当
恒成立,证明:当 时,
时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】条件
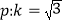 ;条件
;条件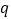 :直线
:直线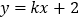 与圆
与圆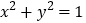 相切,则
相切,则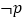 是
是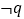 的( )
的( )A. 充分必要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
相关试题

