【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
参考答案:
【答案】
(1)解:由已知得50×(0.0012+0.0024×2+0.0036+x+0.0060)=1,
解得x=0.0044
设该小区100户居民的月均用电量为S,
则S=0.0024×50×75+0.0036×50×125+0.0060×50×175+0.0044×50×225+0.0024×50×275+0.0012×50×325=9+22.5+52.5+49.5+33+19.5=186
(2)该小区用电量在(250,300]的用户数为0.0024×50×100=12,
用电量在(300,350]的用户数为0.0012×50×100=6,
由已知得ξ的可能取值为0,1,2,3,
ξ=0时, ![]() ,
,
ξ=1时, ![]() ,
,
ξ=2时, ![]() ,
,
ξ=3时, ![]()
所以ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
p |
|
|
|
|
E(ξ)=0×p(ξ=0)+1×p(ξ=1)+2×p(ξ=2)+3×p(ξ=3)=1.
【解析】(1)由已知得50×(0.0012+0.0024×2+0.0036+x+0.0060)=1,由此能求出x,由频率分布直方图能求出该小区100户居民的月均用电量.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及期望.
【考点精析】掌握频率分布直方图和离散型随机变量及其分布列是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
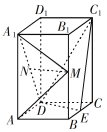
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形三边的长度为连续的三个自然数,则称这样的三角形为“连续整边三角形”。下列说法正确的是( )
A. “连续整边三角形”只能是锐角三角形
B. “连续整边三角形”不可能是钝角三角形
C. 若“连续整边三角形”中最大角是最小角的2倍,则这样的三角形有且仅有1个
D. 若“连续整边三角形”中最大角是最小角的2倍,则这样的三角形可能有2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若 ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地生产某种产品,他们可以调出的数量分别为300吨、750吨.A,B,C三地需要该产品数量分别为200吨,450吨,400吨,甲地运往A,B,C三地的费用分别为6元/吨、3元/吨,5元/吨,乙地运往A,B,C三地的费用分别为5元/吨,9元/吨,6元/吨,问怎样调运,才能使总运费最小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】知函数
 ,
,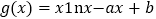 ,
, 与
与 在交点
在交点 处的切线相互垂直.
处的切线相互垂直.(1)求
 的解析式;
的解析式;(2)已知
 ,若函数
,若函数 有两个零点,求
有两个零点,求 的取值范围 .
的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)
 万件与年促销费用
万件与年促销费用 万元(
万元( )满足
)满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将该产品的年利润
 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;(2)该厂家年促销费用投入多少万元时,厂家的利润最大?
相关试题

