【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
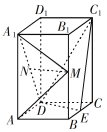
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用三角形中位线和![]() 可证得
可证得![]() ,证得四边形
,证得四边形![]() 为平行四边形,进而证得
为平行四边形,进而证得![]() ,根据线面平行判定定理可证得结论;(2)以菱形
,根据线面平行判定定理可证得结论;(2)以菱形![]() 对角线交点为原点可建立空间直角坐标系,通过取
对角线交点为原点可建立空间直角坐标系,通过取![]() 中点
中点![]() ,可证得
,可证得![]() 平面
平面![]() ,得到平面
,得到平面![]() 的法向量
的法向量![]() ;再通过向量法求得平面
;再通过向量法求得平面![]() 的法向量
的法向量![]() ,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
(1)连接![]() ,
,![]()
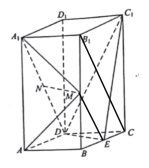
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点 ![]() 为
为![]() 的中位线
的中位线
![]() 且
且![]()
又![]() 为
为![]() 中点,且
中点,且![]()
![]() 且
且![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(2)设![]() ,
,![]()
由直四棱柱性质可知:![]() 平面
平面![]()
![]() 四边形
四边形![]() 为菱形
为菱形 ![]()
则以![]() 为原点,可建立如下图所示的空间直角坐标系:
为原点,可建立如下图所示的空间直角坐标系:
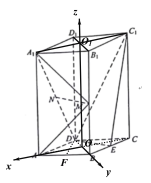
则:![]() ,
,![]() ,
,![]() ,D(0,-1,0)
,D(0,-1,0)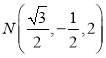
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则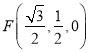
![]() 四边形
四边形![]() 为菱形且
为菱形且![]()
![]() 为等边三角形
为等边三角形 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]()
![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且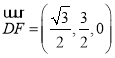
设平面![]() 的法向量
的法向量![]() ,又
,又![]() ,
,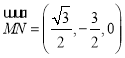
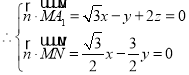 ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
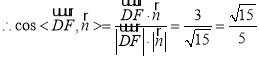
![]()
![]() 二面角
二面角![]() 的正弦值为:
的正弦值为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一矩形花坛
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上, 点在
点在 上,且对角线
上,且对角线 过
过 点,已知
点,已知 米,
米, 米.
米.
(1)要使矩形
 的面积大于50平方米,则
的面积大于50平方米,则 的长应在什么范围?
的长应在什么范围?(2)当
 的长为多少米时,矩形花坛
的长为多少米时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)<
 ,则不等式f(x2)<
,则不等式f(x2)<  的解集为 .
的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面
 内有不共线的三点到平面
内有不共线的三点到平面 的距离相等,则
的距离相等,则 ;④过平面
;④过平面 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面 垂直.其中正确的是( )
垂直.其中正确的是( )A. ①③B. ②④C. ①④D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形三边的长度为连续的三个自然数,则称这样的三角形为“连续整边三角形”。下列说法正确的是( )
A. “连续整边三角形”只能是锐角三角形
B. “连续整边三角形”不可能是钝角三角形
C. 若“连续整边三角形”中最大角是最小角的2倍,则这样的三角形有且仅有1个
D. 若“连续整边三角形”中最大角是最小角的2倍,则这样的三角形可能有2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若 ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示.

(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
相关试题

