【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)![]() 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求 ![]() 的期望.
的期望.
参考答案:
【答案】
(1)解:记 ![]() 表示事件:第1次和第二次这两次发球,甲共得
表示事件:第1次和第二次这两次发球,甲共得 ![]() 分,
分, ![]() ;
;
![]() 表示事件:第3次发球,甲得1分;
表示事件:第3次发球,甲得1分;
![]() 表示事件:开始第4次发球时,甲乙的比分为1比2.
表示事件:开始第4次发球时,甲乙的比分为1比2.
![]() .
.
![]()
![]()
(2)解: ![]() .
.
![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
![]() .
.
![]() .
.
![]() .
.
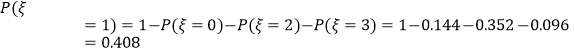 .(或
.(或 ![]() )
)
![]()
![]()
【解析】(1)由题意可知甲、乙的比分为1比2,则可能的情况有两种,根据互斥事件与独立事件的概率求法即可得到其概率。(2)根据题意得到ξ 的可能取值,用对立事件的概率公式求出结果然后根据数学期望的公式求出其值即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知等差数列
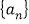 ,
, 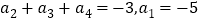 .
.(1)求数列
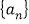 的通项公式;
的通项公式;(2)记数列
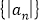 的前
的前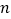 项和为
项和为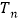 ,求
,求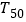 ;
;(3)是否存在正整数
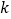 ,使得
,使得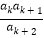 仍为数列
仍为数列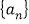 中的项,若存在,求出所有满足的正整数
中的项,若存在,求出所有满足的正整数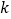 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在一个圆形的六个区域种植观赏植物,要求同一块中种植同一种植物,相邻的两块种植不同的植物,现有4种不同的植物可供选择,则有几种种植方案?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店
A店
B店
C店
售价x(元)
80
86
82
88
84
90
销量y(件)
88
78
85
75
82
66
(1)分别以三家连锁店的平均售价与平均销量为散点,求出售价与销量的回归直线方程 ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附:
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:①若
 ,则
,则  或
或  ;
;
② ,都有
,都有  ;
;
③若 是实数,则
是实数,则  是
是  的充分不必要条件;
的充分不必要条件;
④“ ” 的否定是“
” 的否定是“  ” ;
” ;
其中真命题的个数是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知直线l的参数方程为
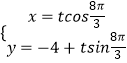 (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为:ρ2﹣3ρ﹣4=0(ρ≥0).
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为:ρ2﹣3ρ﹣4=0(ρ≥0).
(1)写出直线l的普通方程与曲线C的直角坐标系方程;
(2)设直线l与曲线C相交于A,B两点,求∠AOB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数
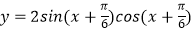 的图象,只需把函数
的图象,只需把函数  的图象上所有的点( )
的图象上所有的点( )
A.向右平行移动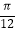 个单位长度
个单位长度
B.向左平行移动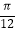 个单位长度
个单位长度
C.向左平行移动 个单位长度
个单位长度
D.向右平行移动 个单位长度
个单位长度
相关试题

