【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
参考答案:
【答案】
(1)解:因为f(x)是奇函数,所以f(0)=0 ![]() =0,解得b=1,
=0,解得b=1,
f(x)= ![]() ,又由f(1)=﹣f(﹣1)
,又由f(1)=﹣f(﹣1) ![]() ,解得a=2
,解得a=2
(2)证明:由(1)可得:f(x)= ![]() =
= ![]() .
.
x1<x2,∴ ![]() >0,
>0,
则f(x1)﹣f(x2)= ![]() =
= ![]() >0,
>0,
∴f(x1)>f(x2).
∴f(x)在R上是减函数
(3)解:∵函数f(x)是奇函数.
∴f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x)成立,
∵f(x)在R上是减函数,∴kx2<1﹣2x,
∴对于任意 ![]() 都有kx2<1﹣2x成立,
都有kx2<1﹣2x成立,
∴对于任意 ![]() 都有k<
都有k< ![]() ,
,
设g(x)= ![]() ,
,
∴g(x)= ![]() =
= ![]() ,
,
令t= ![]() ,t∈[
,t∈[ ![]() ,2],
,2],
则有 ![]() ,∴g(x)min=g(t)min=g(1)=﹣1
,∴g(x)min=g(t)min=g(1)=﹣1
∴k<﹣1,即k的取值范围为(﹣∞,﹣1)
【解析】(1)直接根据函数是奇函数,满足f(﹣x)=﹣f(x),把x=0,和x=1代入,即可得到关于a,b的两个等式,解方程组求出a,b的值.(2)利用减函数的定义即可证明.(3)f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x),即k< ![]() 成立,设g(x)=
成立,设g(x)= ![]() ,
,
换元使之成为二次函数,再求最小值.
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)=
 x3﹣
x3﹣  x2+3x﹣
x2+3x﹣  ,请你根据这一发现,计算f(
,请你根据这一发现,计算f(  )+f(
)+f(  )+f(
)+f(  )+…+f(
)+…+f(  )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位组织职工去某地参观学习,需包车前往,甲车队说:“如果领队买一张全票,其余人可享受7折优惠。”乙车队说:“你们属于团体票,按原价的7.5折优惠。”这两个车队的原价、车型都是一样的,试根据单位去的人数比较两车队的收费哪家更优惠。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)设复数z满足|z|=1,且(3+4i)z为纯虚数,求 ;
;
(2)已知(2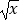 ﹣
﹣ 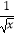 )n的展开式中所有二项式系数之和为64,求展开式的常数项.
)n的展开式中所有二项式系数之和为64,求展开式的常数项. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数中,在(0,+∞)上为增函数的是( )
A.f(x)=3﹣x
B.f(x)=x2﹣3x
C.f(x)=﹣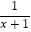
D.f(x)=﹣|x| -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)求广告费支出x与销售额y回归直线方程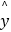 =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b=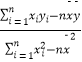 ,
, 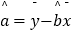
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是
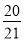 .
.(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量
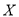 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求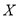 分布列及期望.
分布列及期望.
相关试题

