【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若对任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,
,
求数列![]() 的通项公式.
的通项公式.
参考答案:
【答案】(1)见解析;(2)(ⅰ)见解析;(2)![]() .
.
【解析】试题分析:(1)当![]() 时,
时,![]() .,再写一式,两式相减,可得数列{an}是以首项为1,公比为3的等比数列,从而可求Sn;
.,再写一式,两式相减,可得数列{an}是以首项为1,公比为3的等比数列,从而可求Sn;
(2)①当![]() 时,
时,![]() ,再写一式,两式相减,可得数列{an}是等差数列,从而可求数列{an}的通项公式;
,再写一式,两式相减,可得数列{an}是等差数列,从而可求数列{an}的通项公式;
②因为![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() , 因为
, 因为![]() ,所以
,所以![]() .又因为
.又因为![]() ,即可得到
,即可得到![]() 的值,进而求出通项.
的值,进而求出通项.
试题解析:
(1)当![]() 时,
时,![]() .①
.①
当![]() 时,
时,![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() .②
.②
①②得:![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
所以![]() .
.
(2)(ⅰ)当![]() 时,
时,![]() .③
.③
当![]() 时,
时,![]() .④
.④
③-④得:![]() ,⑤
,⑤
所以![]() .⑥
.⑥
⑤-⑥得:![]() .
.
因为![]() ,所以
,所以![]() 即
即![]() ,
,
所以![]() 是等差数列.
是等差数列.
(ⅱ)因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .又因为
.又因为![]() ,
,
所以![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() 不符合题意.
不符合题意.
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 满足题意.
满足题意.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx在x=﹣
 与x=1处都取得极值.
与x=1处都取得极值.
(1)求a,b的值;
(2)求曲线y=f(x)在x=2处的切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为
 ,每次考B科合格的概率均为
,每次考B科合格的概率均为  .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(I)求甲恰好3次考试通过的概率;
(II)记甲参加考试的次数为ξ,求ξ的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( )
A.9
B.15
C.18
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】运行如图所示的程序框图,则输出结果为( )
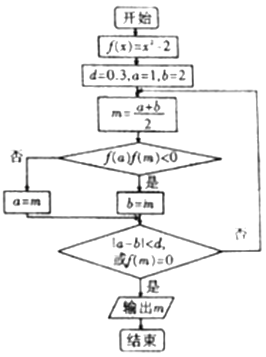
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx
(1)当a=1时,求f(x)的单调区间;
(2)若函数f(x)在(0, )上无零点,求a最小值.
)上无零点,求a最小值.
相关试题

