【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx
(1)当a=1时,求f(x)的单调区间;
(2)若函数f(x)在(0, ![]() )上无零点,求a最小值.
)上无零点,求a最小值.
参考答案:
【答案】
(1)解:当a=1时,f(x)=x﹣1﹣2lnx,
则f′(x)=1﹣ ![]() ,由f′(x)>0,得x>2,
,由f′(x)>0,得x>2,
由f′(x)<0,得0<x<2,
故f(x)的单调减区间为(0,2],单调增区间为[2,+∞).
(2)解:因为f(x)<0在区间(0, ![]() )上恒成立不可能,
)上恒成立不可能,
故要使函数f(x)在(0, ![]() )上无零点,只要对任意的x∈(0,
)上无零点,只要对任意的x∈(0, ![]() ),f(x)>0恒成立,
),f(x)>0恒成立,
即对x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立.
恒成立.
令l(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),
),
则l′(x)= ![]() ,
,
再令m(x)=2lnx+ ![]() ﹣2,x∈(0,
﹣2,x∈(0, ![]() ),
),
则m′(x)=﹣ ![]() +
+ ![]() =
= ![]() <0,
<0,
故m(x)在(0, ![]() )上为减函数,于是m(x)>m(
)上为减函数,于是m(x)>m( ![]() )=2﹣2ln2>0,
)=2﹣2ln2>0,
从而l(x)>0,于是l(x)在(0, ![]() )上为增函数,
)上为增函数,
所以l(x)<l( ![]() )=2﹣4ln2,
)=2﹣4ln2,
故要使a>2﹣ ![]() 恒成立,只要a∈[2﹣4ln2,+∞),
恒成立,只要a∈[2﹣4ln2,+∞),
综上,若函数f(x)在(0, ![]() )上无零点,则a的最小值为2﹣4ln2.
)上无零点,则a的最小值为2﹣4ln2.
【解析】(1)先求出函数f(x)的导数,再令f′(x)>0得单调增区间,令f′(x)<0得单调减区间;(2)先将已知转化为恒成立问题,再利用导数可得函数的单调性,进而可得a的取值范围,从而可得a的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 数列
数列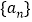 的前
的前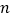 项和,对任意
项和,对任意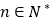 ,都有
,都有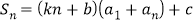 (
(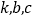 为常数).
为常数).(1)当
 时,求
时,求 ;
;(2)当
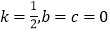 时,
时,(ⅰ)求证:数列
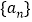 是等差数列;
是等差数列;(ⅱ)若对任意
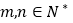 ,必存在
,必存在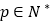 使得
使得 ,已知
,已知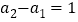 ,且
,且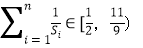 ,
,求数列
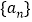 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( )
A.9
B.15
C.18
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】运行如图所示的程序框图,则输出结果为( )
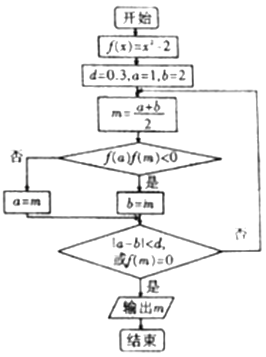
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,  ,
,  (m>0,n>0),若m+n∈[1,2],则
(m>0,n>0),若m+n∈[1,2],则  的取值范围是( )
的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是首项为19,公差为-2的等差数列,Sn为{an}的前n项和.
(1)求通项an及Sn;
(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及前n项和Tn.
相关试题

