【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是等边三角形,且侧面
是等边三角形,且侧面![]() 底面
底面![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
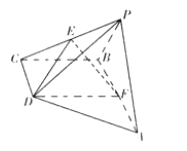
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,
, ![]() ,得到四边形
,得到四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 为
为![]() 的中点.由
的中点.由![]() 为
为![]() 的中点,可得
的中点,可得![]() ,从而证明
,从而证明![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示坐标系,
轴建立如图所示坐标系,
利用向量法能求出平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
试题解析:(Ⅰ)连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,
, ![]() ,
,
∵![]() 且
且![]() ,
, ![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
, ![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 为
为![]() 的中点.
的中点.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)连接![]() ,∵
,∵![]() 为
为![]() 的边
的边![]() 的中点,∴
的中点,∴![]() ,
,
∵平面![]() 底面
底面![]() ,∴
,∴![]() 底面
底面![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示坐标系,
轴建立如图所示坐标系,

设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 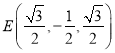 ,
,
∴![]() ,
, 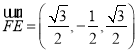 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则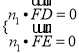 .即
.即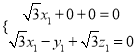 ,
,
令![]() ,得
,得![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 .即
.即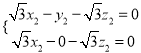 ,
,
令![]() ,得
,得![]() ,
,
设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() (锐角),
(锐角),
则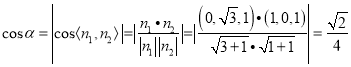 .
.
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
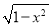 ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y=
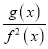 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;(3)设h(x)=|af2(x)﹣
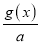 |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
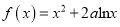 。
。(Ⅰ)求函数
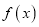 的单调区间;
的单调区间;(Ⅱ)若函数
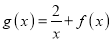 在
在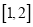 上是减函数,求实数
上是减函数,求实数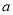 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是
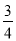 ,乙猜对歌名的概率是
,乙猜对歌名的概率是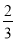 ,丙猜对歌名的概率是
,丙猜对歌名的概率是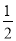 ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量
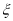 ,求
,求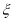 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
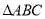 中,内角
中,内角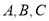 的对边分别是
的对边分别是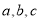 ,已知
,已知 为锐角,且
为锐角,且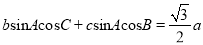 .
.(Ⅰ)求
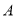 的大小;
的大小;(Ⅱ)设函数
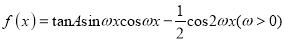 ,其图象上相邻两条对称轴间的距离为
,其图象上相邻两条对称轴间的距离为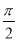 .将函数
.将函数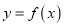 的图象向左平移
的图象向左平移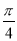 个单位,得到函数
个单位,得到函数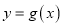 的图象,求函数
的图象,求函数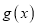 在区间
在区间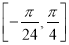 上的值域.
上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数
10环
9环
8环
7环
概率
0.32
0.28
0.18
0.12
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
相关试题

