【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(Ⅰ)![]() ;
;
(Ⅱ)![]() 的分别列为
的分别列为
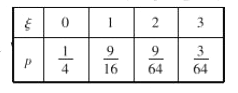
![]() .
.
【解析】试题分析:(1)分别将甲、乙、丙第![]() 次猜对歌名记为事件
次猜对歌名记为事件![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() 相互独立.该小组未能进入第二轮的概率
相互独立.该小组未能进入第二轮的概率![]()
(2)利用相互独立事件的概率计算公式、对立事件的概率计算公式即可得出.
试题解析:
分别将甲、乙、丙第![]() 次猜对歌名记为事件
次猜对歌名记为事件![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() 相互独立.
相互独立.
(Ⅰ)该小组未能进入第二轮的概率![]()
![]() .
.
(Ⅱ)乙猜对歌曲次数![]() 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
![]() ,
,
![]() ,
,
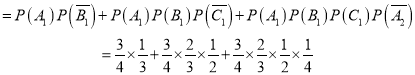
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴![]() 的分别列为
的分别列为
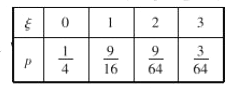
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
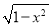 ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y=
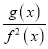 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;(3)设h(x)=|af2(x)﹣
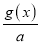 |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
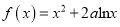 。
。(Ⅰ)求函数
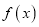 的单调区间;
的单调区间;(Ⅱ)若函数
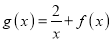 在
在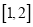 上是减函数,求实数
上是减函数,求实数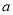 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
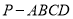 中,底面
中,底面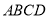 是直角梯形,
是直角梯形, 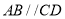 ,
, 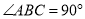 ,
,  ,
, 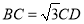 ,
, 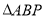 是等边三角形,且侧面
是等边三角形,且侧面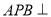 底面
底面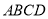 ,
, 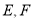 分别是
分别是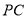 ,
, 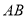 的中点.
的中点.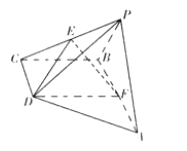
(Ⅰ)求证:
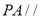 平面
平面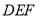 ;
;(Ⅱ)求平面
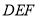 与平面
与平面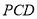 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
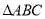 中,内角
中,内角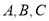 的对边分别是
的对边分别是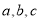 ,已知
,已知 为锐角,且
为锐角,且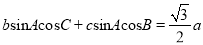 .
.(Ⅰ)求
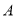 的大小;
的大小;(Ⅱ)设函数
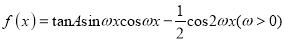 ,其图象上相邻两条对称轴间的距离为
,其图象上相邻两条对称轴间的距离为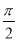 .将函数
.将函数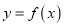 的图象向左平移
的图象向左平移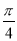 个单位,得到函数
个单位,得到函数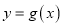 的图象,求函数
的图象,求函数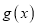 在区间
在区间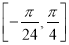 上的值域.
上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数
10环
9环
8环
7环
概率
0.32
0.28
0.18
0.12
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号
分组
频数
频率
第1组
[50,60)
5
0.05
第2组
[60,70)
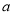
0.35
第3组
[70,80)
30
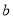
第4组
[80,90)
20
0.20
第5组
[90,100]
10
0.10
合计
100
1.00
(Ⅰ)求
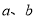 的值;
的值;(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
相关试题

