【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

参考答案:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由切割线定理得EM=EB,其中AE切圆于M,再根据切线长公式得|EA|+|EB|为定值4(2)由椭圆定义可得E,F 均在椭圆![]() 上,由弦长公式化简|EB||FQ|=|BF||EQ|得
上,由弦长公式化简|EB||FQ|=|BF||EQ|得![]() ,设直线EF方程
,设直线EF方程![]() 与椭圆方程联立,结合韦达定理得
与椭圆方程联立,结合韦达定理得![]() ,即证
,即证![]() 成立
成立
试题解析:(1)设AE切圆于M,直线x=4与x轴交于N,则EM=EB
所以![]()
(2)同理FA+FB=4,所以E,F 均在椭圆![]() 上,设EF:
上,设EF: ![]() ,则
,则![]()
与椭圆方程联立得![]()
![]() ,结论成立
,结论成立
-
科目: 来源: 题型:
查看答案和解析>>【题目】在投掷骰子试验中,根据向上的点数可以定义许多事件,如:A={出现1点},B={出现3点或4点},C={出现的点数是奇数},D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖,且不中一等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
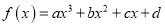 的图象如图所示,则
的图象如图所示,则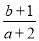 的取值范围是( )
的取值范围是( )
A.
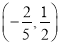 B.
B. 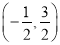 C.
C. 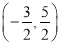 D.
D. 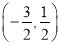
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
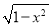 ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y=
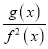 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;(3)设h(x)=|af2(x)﹣
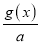 |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
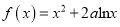 。
。(Ⅰ)求函数
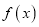 的单调区间;
的单调区间;(Ⅱ)若函数
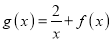 在
在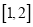 上是减函数,求实数
上是减函数,求实数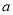 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
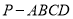 中,底面
中,底面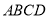 是直角梯形,
是直角梯形, 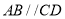 ,
, 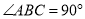 ,
,  ,
, 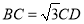 ,
, 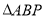 是等边三角形,且侧面
是等边三角形,且侧面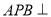 底面
底面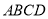 ,
, 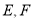 分别是
分别是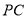 ,
, 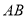 的中点.
的中点.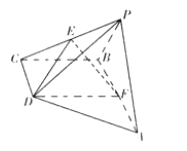
(Ⅰ)求证:
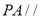 平面
平面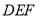 ;
;(Ⅱ)求平面
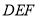 与平面
与平面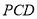 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
相关试题

