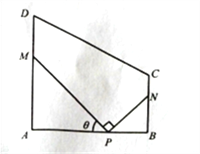
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, ![]() 百米,
百米, ![]() 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且![]() ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),![]() 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, ![]() 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设![]() .
.
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
参考答案:
【答案】(1) 绿化草坪面积的最大值为 平方百米;(2)
平方百米;(2) ![]() 时总美化费用最低为4万元.
时总美化费用最低为4万元.
【解析】试题分析:(1)先求得![]()
![]() ,再利用均值不等式求得正解;(2)先求得
,再利用均值不等式求得正解;(2)先求得![]() ,
, ![]()
总美化费用为![]() ,再利用导数工具求得正解.
,再利用导数工具求得正解.
试题解析:(1)在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
所以绿化草坪面积![]()
![]()
![]()
![]()
又因为![]()
当且当![]() ,即
,即![]() 。此时
。此时![]()
所以绿化草坪面积的最大值为 平方百米.
平方百米.
(2)方法一:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以总美化费用为![]()
![]()
![]()
令![]() 得
得![]() 列表如下
列表如下
|
|
|
|
|
|
| - | 0 | - | ||
|
| 单调递减 |
| 单调递增 |
|
所以当![]() 时,即
时,即![]() 时总美化费用最低为4万元。
时总美化费用最低为4万元。
方法二:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以总美化费用为![]()
![]()
令 得
得![]()
所以![]() ,
, 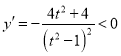
所以![]() 在
在 上是单调递减
上是单调递减
所以当![]() ,
, ![]() 时,即
时,即![]() 时总美化费用最低为4万元。
时总美化费用最低为4万元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的
 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 .
.优秀
非优秀
合计
甲班
10
乙班
30
合计
110
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
 。
。
0.100
0.050
0.025
0.010
0.001
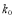
2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数
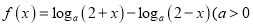 且
且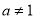 .
. (1)求
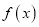 定义域;
定义域;(2)判断
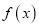 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)求使
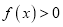 的
的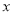 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
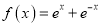 ,其中
,其中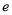 是自然对数的底数.
是自然对数的底数.(1)证明
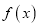 是
是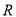 上的偶函数
上的偶函数(2)若关于
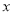 的不等式
的不等式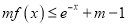 在
在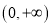 上恒成立,求实数
上恒成立,求实数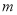 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中
(1)当
 时,求函数
时,求函数 在
在 上的值域;
上的值域;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
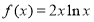 ,
, .
.(1)如果函数
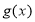 的单调递减区间为
的单调递减区间为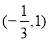 ,求函数
,求函数 的解析式;
的解析式;(2)在(1)的条件下,求函数
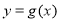 的图象在点
的图象在点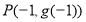 处的切线方程;
处的切线方程;(3)已知不等式
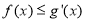
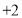 恒成立,若方程
恒成立,若方程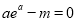 恰有两个不等实根,求
恰有两个不等实根,求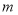 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大,最大月收益是多少?
相关试题

