【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)已知不等式![]()
![]() 恒成立,若方程
恒成立,若方程![]() 恰有两个不等实根,求
恰有两个不等实根,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)![]()
![]()
![]() 的解集为
的解集为![]()
![]()
![]() 的两根分别是
的两根分别是![]() ,
,![]()
![]()
![]()
![]()
![]() ;(2)由(1)知
;(2)由(1)知![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 处的切线斜率
处的切线斜率![]()
![]() 函数
函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]()
![]() 即
即![]() ;(3)由题意知
;(3)由题意知![]() 对
对![]() 上恒成立,设
上恒成立,设![]() ,再由导数工具取得
,再由导数工具取得![]()
![]()
![]() .令
.令![]()
![]()
![]()
![]()
![]() 在
在![]() 递减,在
递减,在![]() 递增,∵
递增,∵![]() ,
,![]() ,当
,当![]() 时,
时,![]()
![]()
![]()
![]() 只需
只需![]() .
.
试题解析: (1)![]() ,
,
由题意![]() 的解集为
的解集为![]() ,
,
即![]() 的两根分别是
的两根分别是![]() ,
,![]() ,
,
代入得![]() ,
,
∴![]() .
.
(2)由(1)知,![]() ,∴
,∴![]() ,
,![]() ,
,
∴点![]() 处的切线斜率
处的切线斜率![]() ,
,
∴函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(3)由题意知![]() 对
对![]() 上恒成立,
上恒成立,
可得![]() 对
对![]() 上恒成立,
上恒成立,
设![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() ,
,![]() (舍),
(舍),
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,
取得最大值,![]() ,∴
,∴![]() .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
∵![]() ,
,![]() ,当
,当![]() 时,
时,![]()
![]()
![]() ,
,
所以要把方程![]() 恰有两个不等实根,只需
恰有两个不等实根,只需![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
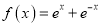 ,其中
,其中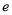 是自然对数的底数.
是自然对数的底数.(1)证明
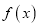 是
是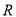 上的偶函数
上的偶函数(2)若关于
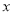 的不等式
的不等式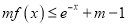 在
在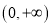 上恒成立,求实数
上恒成立,求实数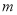 的取值范围.
的取值范围. -
科目: 来源: 题型:
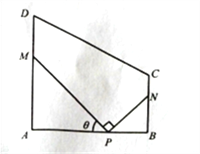
查看答案和解析>>【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC,
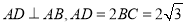 百米,
百米, 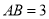 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且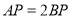 ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),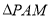 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, 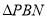 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设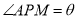 .
.(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中
(1)当
 时,求函数
时,求函数 在
在 上的值域;
上的值域;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大,最大月收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 其中
其中 ,集合
,集合 .
.(1)若
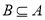 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
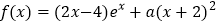 (
(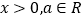 ,
,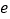 是自然对数的底数).
是自然对数的底数).(1)若
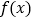 是
是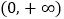 上的单调递增函数,求实数
上的单调递增函数,求实数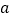 的取值范围;
的取值范围;(2)当
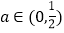 时,证明:函数
时,证明:函数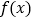 有最小值,并求函数
有最小值,并求函数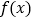 最小值的取值范围.
最小值的取值范围.
相关试题

