【题目】已知:函数![]() 且
且![]() .
.
(1)求![]() 定义域;
定义域;
(2)判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)求使![]() 的
的![]() 的解集.
的解集.
参考答案:
【答案】(1)![]() ;(2)是奇函数;(3)
;(2)是奇函数;(3)![]() .
.
【解析】试题分析:(1)利用对数函数的指数大于零,列出不等式组,解不等式组即可求解函数的定义域.(2)利用对数的运算法则可得![]() ,结合函数的定义域关于原点对称,可得
,结合函数的定义域关于原点对称,可得![]() 为奇函数.(3)利用对数函数的单调性与定义域化简不等式即可求解不等式.
为奇函数.(3)利用对数函数的单调性与定义域化简不等式即可求解不等式.
试题解析:(1)由题意得 ![]() ,即﹣2<x<2.∴f(x)的定义域为(﹣2,2);
,即﹣2<x<2.∴f(x)的定义域为(﹣2,2);
(2)∵对任意的x∈(﹣2,2),﹣x∈(﹣2,2)
f(﹣x)=loga(2﹣x)﹣loga(2+x)=﹣f(x),
∴f(x)=loga(2+x)﹣loga(2﹣x)是奇函数;
(3)f(x)=loga(2+x)﹣loga(2﹣x)>0,即log2(2+x)>loga(2﹣x),
∴当a∈(0,1)时,可得2+x<2﹣x,即﹣2<x<0.
当a∈(1,+∞)时,可得2+x>2﹣x,即x∈(0,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店购进某种水果的成本为
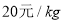 ,经过市场调研发现,这种水果在未来30天的销售单价
,经过市场调研发现,这种水果在未来30天的销售单价 与时间
与时间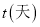 之间的函数关系式为
之间的函数关系式为 ,销售量
,销售量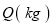 与时间
与时间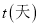 的函数关系式为
的函数关系式为 。
。(Ⅰ)该水果店哪一天的销售利润最大?最大利润是多少?
(Ⅱ)为响应政府“精准扶贫”号召,该店决定每销售
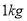 水果就捐赠
水果就捐赠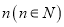 元给“精准扶贫”对象.欲使捐赠后不亏损,且利润随时间
元给“精准扶贫”对象.欲使捐赠后不亏损,且利润随时间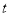
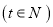 的增大而增大,求捐赠额
的增大而增大,求捐赠额 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】《国务院关于修改〈中华人民共和国个人所得税法实施条例〉的决定》已于2008年3月1日起施行,个人所得税税率表如下:
级数
全月应纳税所得额
税率
1
不超过500元的部分
5%
2
超过500至2 000元的部分
10%
3
超过2 000元至5 000元的部分
15%
…
…
…
9
超过100 000元的部分
45%
注:本表所示全月应纳税所得额为每月收入额减去2 000元后的余额.
(1)若某人2008年4月份的收入额为4 200元,求该人本月应纳税所得额和应纳的税费;
(2)设个人的月收入额为x元,应纳的税费为y元.当0<x≤3 600时,试写出y关于x的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的
 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 .
.优秀
非优秀
合计
甲班
10
乙班
30
合计
110
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
 。
。
0.100
0.050
0.025
0.010
0.001
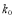
2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
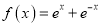 ,其中
,其中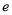 是自然对数的底数.
是自然对数的底数.(1)证明
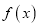 是
是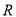 上的偶函数
上的偶函数(2)若关于
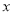 的不等式
的不等式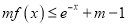 在
在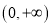 上恒成立,求实数
上恒成立,求实数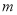 的取值范围.
的取值范围. -
科目: 来源: 题型:
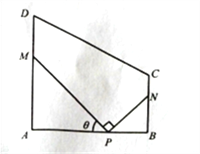
查看答案和解析>>【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC,
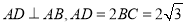 百米,
百米, 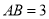 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且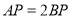 ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),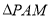 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, 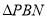 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设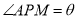 .
.(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中
(1)当
 时,求函数
时,求函数 在
在 上的值域;
上的值域;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的取值范围.
的取值范围.
相关试题

