【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大,最大月收益是多少?
参考答案:
【答案】见解析
【解析】(1)当每辆车的月租金定为![]() 元时,未租出的车为
元时,未租出的车为![]() 辆,(2分)
辆,(2分)
![]() ,
,
所以租出了![]() 辆车.(4分)
辆车.(4分)
(2)设每辆车的月租金定为![]() 元,
元,
则租凭公司的月收益为![]() ,(6分)
,(6分)
整理得![]() ,(8分)
,(8分)
所以当![]() 时,
时,![]() 最大,其最大值为
最大,其最大值为![]() ,(10分)
,(10分)
答:当每辆车的月租金定为![]() 元时,租赁公司的月收益最大,最大月收益是
元时,租赁公司的月收益最大,最大月收益是![]() 元.(12分)
元.(12分)
-
科目: 来源: 题型:
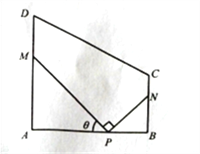
查看答案和解析>>【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC,
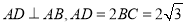 百米,
百米, 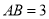 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且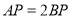 ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),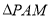 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场,  区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设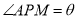 .
.(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中
(1)当
 时,求函数
时,求函数 在
在 上的值域;
上的值域;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
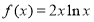 ,
, .
.(1)如果函数
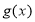 的单调递减区间为
的单调递减区间为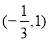 ,求函数
,求函数 的解析式;
的解析式;(2)在(1)的条件下,求函数
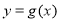 的图象在点
的图象在点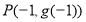 处的切线方程;
处的切线方程;(3)已知不等式
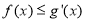
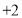 恒成立,若方程
恒成立,若方程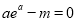 恰有两个不等实根,求
恰有两个不等实根,求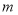 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 其中
其中 ,集合
,集合 .
.(1)若
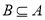 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
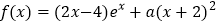 (
(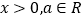 ,
,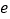 是自然对数的底数).
是自然对数的底数).(1)若
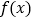 是
是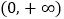 上的单调递增函数,求实数
上的单调递增函数,求实数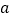 的取值范围;
的取值范围;(2)当
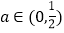 时,证明:函数
时,证明:函数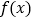 有最小值,并求函数
有最小值,并求函数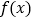 最小值的取值范围.
最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
]
组别
PM2.5浓度(微克/立方米)
频数(天)
频率
第一组
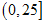
3
0.15
第二组
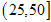
12
0.6
第三组
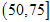
3
0.15
第四组
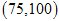
2
0.1
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
相关试题

