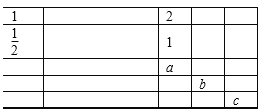
【题目】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】A
【解析】
从第三列入手,根据等比中项得2×a=12,可得a=![]() ,所以每一列的公比都为
,所以每一列的公比都为![]() ,由此计算出第一列中的第3个数为
,由此计算出第一列中的第3个数为![]() =
=![]() .接下来研究第三行对应的等差数列,可以求出公差为
.接下来研究第三行对应的等差数列,可以求出公差为![]() (
(![]() )=
)=![]() ,从而用等差数列的通项公式计算出第三行的第4、5两个数,也即第四列的第3个数和第五列的第3个数.最后研究第四列和第五列的等比数列,分别可以计算出b、c的值,最终求出的a+b+c值.
,从而用等差数列的通项公式计算出第三行的第4、5两个数,也即第四列的第3个数和第五列的第3个数.最后研究第四列和第五列的等比数列,分别可以计算出b、c的值,最终求出的a+b+c值.
∵每一横行成等差数列,每一纵列成等比数列,
∴根据第三列,得2×a=12,可得a=![]() ,所以公比q=
,所以公比q=![]()
在第一列中,第三个数为![]() =
=![]()
因此根据等差中项得:第三行第2个数为:![]() =
=![]()
可得第三行等差数列的公差为d=![]() =
=![]()
∴在第三行中,第4个数为:![]() +3×
+3×![]() =
=![]() ,第5个数为:
,第5个数为:![]() +4×
+4×![]() =
=![]() ,
,
即第四列中,第3个数为![]() ;第五列中,第3个数为
;第五列中,第3个数为![]() .
.
∵在第四列中,第4个数b与第3个数之比为q=![]()
∴b=![]()
同理,在第五列中,第5个数c与第3个数之比为q2=![]()
∴c=![]()
综上所述,得a+b+c=![]() =1
=1
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin2x的图象先向左平移
 个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
A.
B.y=2cos2x
C.y=2sin2x
D.y=cosx -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml以上为常喝,体重超过50kg为肥胖。
常喝
不常喝
合计
肥胖
6
2
8
不肥胖
4
18
22
合计
10
20
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
 。
。(1)是否有
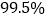 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由(2)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:

(参考公式:
 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别
频数
频率
[145.5,149.5)
1
0.02
[149.5,153.5)
4
0.08
[153.5,157.5)
20
0.40
[157.5,161.5)
15
0.30
[161.5,165.5)
8
0.16
[165.5,169.5)
m
n
合 计
M
N

(1)求出表中
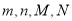 所表示的数;
所表示的数;(2)画出频率分布直方图;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程
 正实数解有且仅有一个,那么实数a的取值范围为( )
正实数解有且仅有一个,那么实数a的取值范围为( )
A.{a|a≤0}
B.{a|a≤0或a=2}
C.{a|a≥0}
D.{a|a≥0或a=﹣2} -
科目: 来源: 题型:
查看答案和解析>>【题目】如果
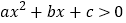 的解集为
的解集为 ,则对于函数
,则对于函数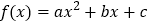 应有
应有 ( )
A.
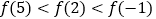 B.
B. 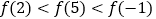
C.
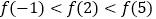 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为等比数列
为等比数列 的前
的前 项和,
项和, ,若数列
,若数列 也是等比数列,则
也是等比数列,则 等于( )
等于( )A. 2n B. 3n C.
 D.
D. 
相关试题

