【题目】已知集合P={x|2x2﹣5x+2≤0},函数y=log2(ax2+2)的定义域为S
(1)若P∩S≠,求实数a的取值范围
(2)若方程log2(ax2+2)=2在 ![]() 上有解,求实数a的取值范围.
上有解,求实数a的取值范围.
参考答案:
【答案】
(1)解:集合P={x|2x2﹣5x+2≤0}={x| ![]() },由已知Q={x|ax2+2>0},若P∩Q≠,
},由已知Q={x|ax2+2>0},若P∩Q≠,
则说明在[ ![]() ,2]内至少有一个x值,使不等式ax2+2>0,即,
,2]内至少有一个x值,使不等式ax2+2>0,即,
在[ ![]() ,2]内至少有一个x值,使a>﹣
,2]内至少有一个x值,使a>﹣ ![]() 成立,﹣
成立,﹣ ![]() 的最小值为:﹣8,
的最小值为:﹣8,
∴a的取值范围是a>﹣8;
(2)解:∵方程log2(ax2+2)=2在 ![]() 上内有解,
上内有解,
∴ax2+2=4即ax2﹣2=0在 ![]() 内有解,分离a与x,得a=
内有解,分离a与x,得a= ![]() ∈
∈ ![]() .
.
即a的取值范围是: ![]() .
.
【解析】(1)是一个存在性的问题,此类题求参数一般转化为求最值.若是存在大于某式的值成立,一般令其大于其最小值,(2)也是一个存在性的问题,其与(1)不一样的地方是其为一个等式,故应求出解析式对应函数的值域,让该参数是该值域的一个元素即可保证存在性.
【考点精析】根据题目的已知条件,利用集合的交集运算的相关知识可以得到问题的答案,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
甲
0
1
0
2
2
0
3
1
2
4
乙
2
3
1
1
0
2
1
1
0
1
由此判断性能较好的一台是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
0.025
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
②
[145,155]
0.050
合计
③
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面多边形
 中,四边形
中,四边形 为正方形,
为正方形,  ,
,  ,沿着
,沿着 将图形折成图2,其中
将图形折成图2,其中 ,
,  ,
,  为
为 的中点.
的中点.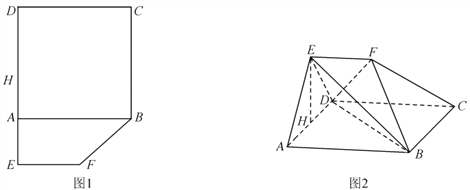
(1)求证:
 ;
;(2)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于 ,
,  两点,以线段
两点,以线段 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )A. 相离 B. 相交 C. 相切 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域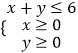 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 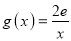 .
.(1)当
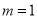 时,求
时,求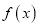 的单调区间;
的单调区间;(2)当
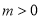 时,若存在
时,若存在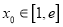 使得
使得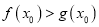 成立,求实数
成立,求实数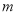 的取值范围.
的取值范围.
相关试题

