【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,若存在
时,若存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() 的单调递增区间为
的单调递增区间为![]() ,不存在单调递减区间;(2)
,不存在单调递减区间;(2) ![]()
【解析】试题分析: (1)当![]() 时,
时, ![]() ,对函数求导,令
,对函数求导,令![]() 解出x的范围,可得函数的单调递增区间为
解出x的范围,可得函数的单调递增区间为![]() ,即定义域内单调递增;(2) 据题意,得
,即定义域内单调递增;(2) 据题意,得![]() 在
在![]() 上有解,设
上有解,设![]() ,则
,则![]() 的最小值大于0,对函数求导判断单调性,进而得出最小值,解出m的范围即可.
的最小值大于0,对函数求导判断单调性,进而得出最小值,解出m的范围即可.
试题解析:
(1)当![]() 时,
时, ![]() ,所以
,所以![]()
![]() .
.
所以当![]() 时,
时, ![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,不存在单调递减区间.
,不存在单调递减区间.
(2)据题意,得![]() 在
在![]() 上有解,
上有解,
设![]()
![]() ,
,
则![]() ,所以当
,所以当![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时, ![]() ,
,
解得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
点睛: 本题考查函数导数与单调性,恒成立有解问题.方程的有解问题可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={x|2x2﹣5x+2≤0},函数y=log2(ax2+2)的定义域为S
(1)若P∩S≠,求实数a的取值范围
(2)若方程log2(ax2+2)=2在 上有解,求实数a的取值范围.
上有解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于 ,
,  两点,以线段
两点,以线段 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )A. 相离 B. 相交 C. 相切 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域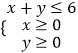 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是递增的等差数列a3=
 ,且a2a4=6.
,且a2a4=6.
(1)求{an}的首项a1和公差d;
(2)求{an}的通项和前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的方程为x=﹣2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
(1)过M点的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的 ,求直线l1的方程;
,求直线l1的方程;
(2)若椭圆中a,c满足 =2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
=2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
(3)过M点作直线l2与圆相切于点N,设(2)中椭圆的两个焦点分别为F1 , F2 , 求三角形△NF1F2面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
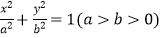 ,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线
,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线 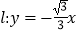 被圆A和圆B截得的弦长之比为
被圆A和圆B截得的弦长之比为 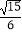 ;
; 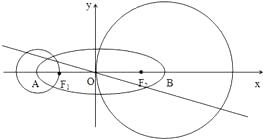
(1)求椭圆C的离心率;
(2)己知a=7,问是否存在点P,使得过P点有无数条直线被圆A和圆B截得的弦长之比为 ;若存在,请求出所有的P点坐标;若不存在,请说明理由.
;若存在,请求出所有的P点坐标;若不存在,请说明理由.
相关试题

