【题目】在平面直角坐标系xOy中,已知直线l的参数方程为 ![]() (t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
(t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ= ![]() (p>0).
(p>0).
(Ⅰ)写出直线l的极坐标方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,求 ![]() +
+ ![]() 的值.
的值.
参考答案:
【答案】解:(I)由 ![]() 得
得  ,∴直线l的普通方程为
,∴直线l的普通方程为 ![]() ﹣
﹣ ![]() =0,即sinαx﹣cosαy=0. 把x=ρcosθ,y=ρsinθ代入普通方程得sinαρcosθ﹣cosαρsinθ=0.
=0,即sinαx﹣cosαy=0. 把x=ρcosθ,y=ρsinθ代入普通方程得sinαρcosθ﹣cosαρsinθ=0.
∵ρ= ![]() ,∴p=ρ﹣ρcosθ=ρ﹣x,∴ρ=p+x,两边平方得ρ2=x2+2px+p2 , ∴x2+y2=x2+2px+p2 , 即y2﹣2px﹣p2=0.
,∴p=ρ﹣ρcosθ=ρ﹣x,∴ρ=p+x,两边平方得ρ2=x2+2px+p2 , ∴x2+y2=x2+2px+p2 , 即y2﹣2px﹣p2=0.
(II)联立方程组 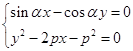 ,解得
,解得 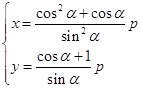 或
或 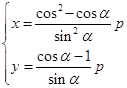 .
.
∴|OA|2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ,|OB|2=(
,|OB|2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ,
,
∴|OA|= ![]() ,|OB|=
,|OB|= ![]() .
.
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() (
( ![]() +
+ ![]() )=
)= ![]()
【解析】(1)分别用x,y表示t,消去参数得到普通方程,再化为极坐标方程;(2)联立方程组解出A,B坐标,代入两点间的距离公式得出|OA|,|OB|,再进行化简计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形
 的三边长是公差为2的等差数列,且最大角的正弦值为
的三边长是公差为2的等差数列,且最大角的正弦值为 ,则这个三角形的周长是( )
,则这个三角形的周长是( )A. 18 B. 15 C. 21 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x+1)ex和函数g(x)=(ex﹣a)(x﹣1)2(a>0)(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)判断函数g(x)的极值点的个数,并说明理由;
(3)若函数g(x)存在极值为2a2 , 求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
(Ⅰ)证明:C,E,F,D四点共圆;
(Ⅱ)若D为BC的中点,且AF=3,FD=1,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的最小值和最小正周期;
的最小值和最小正周期;(Ⅱ)已知
 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥
 中,
中, 为
为 中点,
中点, 为
为 中点,且
中点,且 为正三角形.
为正三角形.(I)求证:
 平面
平面 ;
;(II)求证:平面
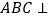 平面
平面 ;
;(III)若
 ,求三棱锥
,求三棱锥 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第
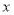 天的实验需投入实验费用为
天的实验需投入实验费用为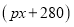 元
元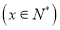 ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.(1)求
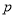 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;(2)现有某知名企业对该项实验进行赞助,实验
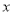 天共赞助
天共赞助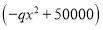 元
元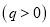 .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求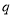 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
相关试题

